
写出下列函数的单调增区间:
(1)y=3sin(2x-![]() );(2)y=2cos(2x+
);(2)y=2cos(2x+![]() );(3)y=logi[sin(2x+
);(3)y=logi[sin(2x+![]() )].
)].
|
思路分析:应用正、余弦函数的单调性.(1)设z=2x- 解:(1)设z=2x- 即2x- 由- 得- 即- 所以,函数y=3sin(2x- (2)由-π+2kπ≤2x+ 即- 所以,函数y=2cos(2x+ (3)设u=sin(2x+ 由y=sinx(y>0)的图象,可知y=sinx(y>0)的增区间为(2kπ,2kπ+ 2kπ<2x+ 所以- 所以,函数y=log2[sin(2x+ 方法归纳:本题的关键在于转化思想的应用,使用了整体换元法.函数的单调性是函数在定义域内的某个区间上的性质,因此,要求函数的单调区间,应首先求函数的定义域.此外,函数的单调区间应写成区间的形式. |


科目:高中数学 来源:2010年江苏省高一第一学期阶段测试数学试卷 题型:填空题
下列结论中:
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)也是增函数,则函数f(x)在R上是增函数;
②若f(2)=f(-2),则函数f(x)不是奇函数;
③函数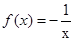 的单调增区间是(-∞,0)
的单调增区间是(-∞,0) (0,+∞)
(0,+∞)
④对应法则和值域相同的函数的定义域也相同;
⑤函数的定义域一定不是空集; 写出上述所有正确结论的序号: ▲ .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
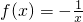 的单调增区间是(-∞,0)∪(0,+∞)
的单调增区间是(-∞,0)∪(0,+∞)查看答案和解析>>
科目:高中数学 来源:2010年江苏省沭阳中学高一第一学期阶段测试数学试卷 题型:填空题
下列结论中:
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)也是增函数,则函数f(x)在R上是增函数;
②若f(2)=f(-2),则函数f(x)不是奇函数;
③函数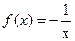 的单调增区间是(-∞,0)
的单调增区间是(-∞,0)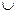 (0,+∞)
(0,+∞)
④对应法则和值域相同的函数的定义域也相同;
⑤函数的定义域一定不是空集; 写出上述所有正确结论的序号: ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com