
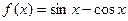 ,
,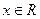 .(1)求函数
.(1)求函数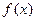 在
在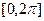 内的单调递增区间;
内的单调递增区间;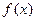 在
在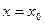 处取到最大值,求
处取到最大值,求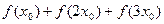 的值;
的值;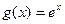 (
(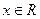 ),求证:方程
),求证:方程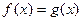 在
在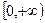 内没有实数解.(参考数据:
内没有实数解.(参考数据: ,
,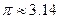 )
) 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源:不详 题型:解答题
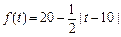 (元).
(元).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
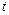 元(其中
元(其中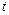 为常数,且
为常数,且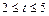 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为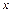 元(
元(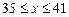 ),根据市场调查,日销售量与
),根据市场调查,日销售量与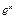 (
(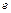 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.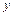 (元)与每件玩具的出厂价
(元)与每件玩具的出厂价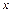 元的函数关系式;
元的函数关系式;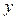 最大,并求
最大,并求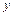 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
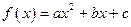 .
.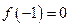 ,试判断函数
,试判断函数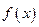 零点个数;
零点个数;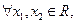 且
且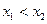 ,
,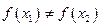 ,试证明
,试证明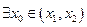 ,使
,使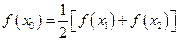 成立。
成立。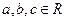 ,使
,使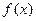 同时满足以下条件①对
同时满足以下条件①对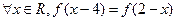 ,且
,且 ;②对
;②对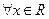 ,都有
,都有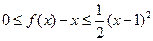 。若存在,求出
。若存在,求出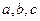 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
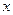 艘产值函数为
艘产值函数为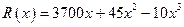 (单位:万元),成本函数
(单位:万元),成本函数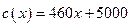 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数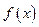 的边际函数
的边际函数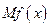 定义为
定义为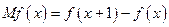
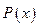 及边际利润函数
及边际利润函数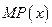 (利润=产值—成本)
(利润=产值—成本)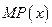
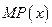 的单调递减区间
的单调递减区间查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
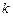 和
和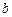 ,使得函数
,使得函数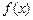 和
和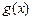 对其定义域上的任意实数
对其定义域上的任意实数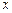 分别满足:
分别满足: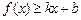 和
和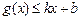 ,则称直线
,则称直线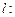
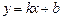 为
为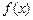 和
和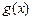 的“隔离直线”.已知
的“隔离直线”.已知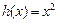 ,
,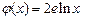 (其中
(其中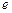 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断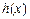 与
与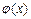 间的隔离直线方程为 .
间的隔离直线方程为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com