已知
,
,
求证：
.
证明： ∴ 即 又 ∴ 由二倍角公式可推出半角公式，由两角和现差的三角公式可推出和差化积公式及积化和差公式. ⑴半角公式： ⑵和差化积公式： ⑶积化和差公式； 这些公式不要求同学们记忆，但它因更深层地揭示了单角和复角的关系，所以有些题在单角和复角互化过程中，用这些公式比较简单. 如，求证： 分析：左边为单角，右边含有复角，因此从统一角入手. 证法一：左边 证法二：右式 注：两种方法中，分母都通过和差化积与积化和差进行了角的转换，做起来较简单.
|
分析：这是一道三角与代数的综合题，对A与B的表达式进行统一角及名是本题的关键.
|
超能学典应用题题卡系列答案科目：高中数学 来源：2010-2011学年福建省龙岩市高三上学期期末考试数学理卷（一级学校） 题型：解答题
（本题满分14分）
已知函数
.
（Ⅰ）若
为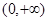
上的单调函数，试确定实数
的取值范围;[来源:学_科_网Z_X_X_K]
（Ⅱ）求函数在定义域上的极值；
（Ⅲ）设
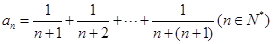,求证：
.
查看答案和解析>>
科目：高中数学 来源：2010-2011学年福建省龙岩市高三第一次教学质量检测一级达标校数学理卷 题型：解答题
（本题满分14分）
已知函数
.
（Ⅰ）若
为
上的单调函数，试确定实数
的取值范围;
（Ⅱ）求函数在定义域上的极值；
（Ⅲ）设
,求证：
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.
.
,
.故原左式
.
,
左边.∴原式成立.
，
，
.
,
,
,
.
，
，
，
.
.
右边.
.
.
.
的单调递减区间.
的x的集合.