
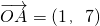 ,
,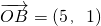 ,
,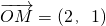 ,点P是直线OM上的一个动点,且
,点P是直线OM上的一个动点,且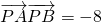 ,求
,求 的坐标及∠APB的余弦值.
的坐标及∠APB的余弦值.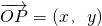 ,∵点P在直线OM上,
,∵点P在直线OM上, 与
与 共线,而
共线,而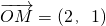 ,
, =(2y,y),
=(2y,y), =
= -
- =(1-2y,7-y),
=(1-2y,7-y), =
= -
- =(5-2y,1-y),
=(5-2y,1-y), =(1-2y)(5-2y)+(7-y)(1-y),即
=(1-2y)(5-2y)+(7-y)(1-y),即 =5y2-20y+12,
=5y2-20y+12, =-8,
=-8, =(4,2),
=(4,2), =(-3,5),
=(-3,5), =(1,-1),
=(1,-1),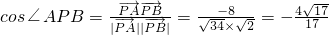
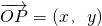 ,再由点P在直线OM上,得到
,再由点P在直线OM上,得到 与
与 共线,由此共线条件得到x,y之间的关系,代入
共线,由此共线条件得到x,y之间的关系,代入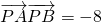 ,解出x,y的值,即可求出
,解出x,y的值,即可求出 的坐标及
的坐标及 =(-3,5),
=(-3,5), =(1,-1),再由夹角的向量表示公式
=(1,-1),再由夹角的向量表示公式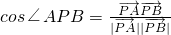 求出∠APB的余弦值
求出∠APB的余弦值

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| OM |
| PA |
| PB |
| OP |
| OA |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OM |
| PA |
| PB |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OM |
| PA |
| PB |
| OP |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com