
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(I)由直角三角形可得![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() ,从而可得
,从而可得![]() 平面
平面![]() 进而可得结论;(II)以
进而可得结论;(II)以![]() 点为坐标原点,
点为坐标原点, ![]() 分别
分别![]() 轴建立空间直角坐标系,分别求出平面
轴建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果.
的一个法向量,根据空间向量夹角余弦公式,可得结果.
试题解析:(I)由![]() ,可得
,可得![]() ,
,
又![]()
从而![]() ,
, ![]() 底面
底面![]() ,
, ![]()
![]() ,
, ![]() 平面
平面![]() 所以平面
所以平面![]() 平面
平面![]() .
.
(II)由(I)可知![]() 为
为![]() 与底面
与底面![]() 所成角.
所成角.
所以![]() ,所以
,所以![]()
又![]() 及
及![]() ,可得
,可得![]() ,
,
以![]() 点为坐标原点,
点为坐标原点, ![]() 分别
分别![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() .
.
设平面![]() 的法向量
的法向量![]() .
.
则由![]() 得
得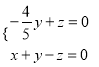 取
取![]()
同理平面![]() 的法向量为
的法向量为![]()
所以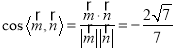
又二面角![]() 为锐角.所以二面角
为锐角.所以二面角![]() 余弦值为
余弦值为![]() .
.
【方法点晴】本题主要考查利用空间垂直关系以及空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中, ![]() ,
, ![]() 两点的坐标分别为
两点的坐标分别为![]() ,
, ![]() ,动点
,动点![]() 满足:直线
满足:直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
, ![]() 分别交曲线
分别交曲线![]() 于
于![]() ,
, ![]() 两点,设
两点,设![]() 的斜率为
的斜率为![]() (
(![]() ),
),![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
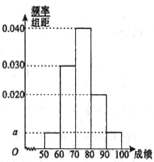
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,有下列说法:
①若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上没有零点;
②若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上可能有零点;
③若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上没有零点;
④若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上至少有一个零点;
其中正确说法的序号是(把所有正确说法的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批材料可以建成100m长的围墙,现用这些材料在一边靠墙的地方围成一块封闭的矩形场地,中间隔成3个面积相等的小矩形(如图),则围成的矩形场地的最大总面积为(围墙厚度忽略不计)m2 . 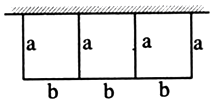
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到点
到点![]() 和直线l:
和直线l: ![]() 的距离相等.
的距离相等.
(Ⅰ)求动点![]() 的轨迹E的方程;
的轨迹E的方程;
(Ⅱ)已知不与![]() 垂直的直线
垂直的直线![]() 与曲线E有唯一公共点A,且与直线
与曲线E有唯一公共点A,且与直线![]() 的交点为
的交点为![]() ,以AP为直径作圆
,以AP为直径作圆![]() .判断点
.判断点![]() 和圆
和圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
, ![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点![]() 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com