
【题目】设函数![]() .
.
(1)当![]() 时,试求
时,试求![]() 的单调增区间;
的单调增区间;
(2)试求![]() 在
在![]() 上的最大值;
上的最大值;
(3)当![]() 时,求证:对于
时,求证:对于![]() 恒成立.
恒成立.
【答案】(1) ![]() ;(2)详见解析; (3)详见解析.
;(2)详见解析; (3)详见解析.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,
, ![]() ,当
,当![]() ,得
,得![]() ,所以
,所以![]() 的单调增区间为
的单调增区间为![]() ;(2)
;(2)![]() ,
, ![]() ,得
,得![]() ,讨论
,讨论![]() ,
, ![]() ,
, ![]() ,利用函数在区间
,利用函数在区间![]() 上的单调性可以求出函数
上的单调性可以求出函数![]() 在
在![]() 上的最大值;(3)当
上的最大值;(3)当![]() 时,设函数
时,设函数![]() ,则问题转化为证明对于
,则问题转化为证明对于![]() ,
, ![]() ,利用导数研究函数
,利用导数研究函数![]() 在区间
在区间![]() 的单调性,从而证明
的单调性,从而证明![]() 成立,于是问题得证.
成立,于是问题得证.
试题解析:(1)由![]() ,得
,得![]() .当
.当![]() 时,
时, ![]() ,令
,令![]() ,得
,得![]() .所以
.所以![]() 的单调增区间为
的单调增区间为![]() .
.
(2)令![]() ,得
,得![]() ,所以当
,所以当![]() 时,
时, ![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减; ![]() 时,
时, ![]() ,
, ![]() 单调递增,综上,无论
单调递增,综上,无论![]() 为何值,当
为何值,当![]() 时,
时, ![]() 最大值都为
最大值都为![]() 或
或![]() .
. ![]() ,
,
![]() ,所以当
,所以当
![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .
.
(3)令![]() ,所以
,所以![]() ,所以
,所以![]() ,令
,令![]() ,
,
解得![]() ,所以当
,所以当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增,所以当
单调递增,所以当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() 恒成立.
恒成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得![]() 分).设每次击鼓出现音乐的概率为
分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两个容器,甲容器容量为![]() ,装满纯酒精,乙容器容量为
,装满纯酒精,乙容器容量为![]() ,其中装有体积为
,其中装有体积为![]() 的水(
的水(![]() :单位:
:单位: ![]() ).现将甲容器中的液体倒人乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒人甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过
).现将甲容器中的液体倒人乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒人甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过![]() 次操作之后,乙容器中含有纯酒精
次操作之后,乙容器中含有纯酒精![]() (单位:
(单位: ![]() ),下列关于数列
),下列关于数列![]() 的说法正确的是( )
的说法正确的是( )
A. 当![]() 时,数列
时,数列![]() 有最大值
有最大值![]()
B. 设![]() ,则数列
,则数列![]() 为递减数列
为递减数列
C. 对任意的![]() ,始终有
,始终有![]()
D. 对任意的![]() ,都有
,都有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.
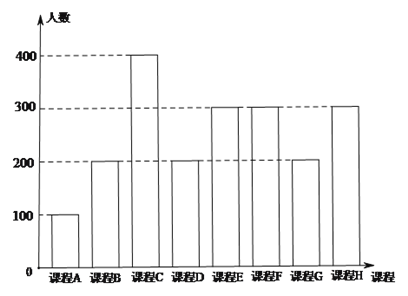
图中,课程![]() 为人文类课程,课程
为人文类课程,课程![]() 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组![]() ”).
”).
(Ⅰ)在“组![]() ”中,选择人文类课程和自然科学类课程的人数各有多少?
”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组![]() ”中选择
”中选择![]() 课
课
程或![]() 课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择
课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择![]() 课程的学生中有
课程的学生中有![]() 人参加科学营活动,每人需缴纳
人参加科学营活动,每人需缴纳![]() 元,选择
元,选择![]() 课程的学生中有
课程的学生中有![]() 人参加该活动,每人需缴纳
人参加该活动,每人需缴纳![]() 元.记选择
元.记选择![]() 课程和
课程和![]() 课程的学生自愿报名人数的情况为
课程的学生自愿报名人数的情况为![]() ,参加活动的学生缴纳费用总和为
,参加活动的学生缴纳费用总和为![]() 元.
元.
①当![]() 时,写出
时,写出![]() 的所有可能取值;
的所有可能取值;
②若选择![]() 课程的同学都参加科学营活动,求
课程的同学都参加科学营活动,求![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com