
设向量a=(2,sin θ),b=(1,cos θ),θ为锐角.
(1)若a·b=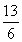 ,求sin θ+cos θ的值;
,求sin θ+cos θ的值;
(2)若a∥b,求sin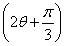 的值.
的值.
(1)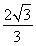 (2)
(2)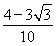
【解析】(1)因为a·b=2+sin θcos θ=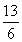 ,
,
所以sin θcos θ=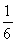 .(2分)
.(2分)
所以(sin θ+cos θ)2=1+2sin θcos θ=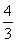 .
.
又因为θ为锐角,所以sin θ+cos θ=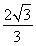 .(5分)
.(5分)
(2)法一:因为a∥b,所以tan θ=2.(7分)
所以sin 2θ=2sin θcos θ= ,cos 2θ=cos2θ-sin2θ=
,cos 2θ=cos2θ-sin2θ=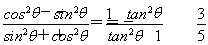 .(11分)
.(11分)
所以sin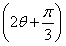 =
=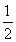 sin 2θ+
sin 2θ+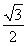 cos 2θ=
cos 2θ=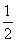 ×
×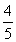 +
+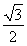 ×
×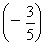 =
=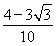 .(14分)
.(14分)
法二 因为a∥b,所以tan θ=2.(7分)
所以sin θ=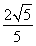 ,cos θ=
,cos θ=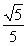 .
.
因此sin 2θ=2sin θcos θ=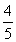 ,
,
cos 2θ=cos2θ-sin2θ=-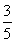 .(11分)
.(11分)
所以sin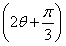 =
=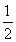 sin 2θ+
sin 2θ+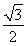 cos 2θ=
cos 2θ=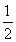 ×
×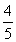 +
+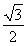 ×
×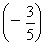 =
=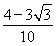 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:填空题
在等差数列{an}中,已知a3+a8=10,则3a5+a7=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:填空题
已知集合A={x|x2-x≤0},函数f(x)=2-x(x∈A)的值域为B,则(∁RA)∩B=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练D组练习卷(解析版) 题型:解答题
已知△ABC中,角A,B,C的对边分别为a,b,c,且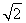 acos B=ccos B+bcos C.
acos B=ccos B+bcos C.
(1)求角B的大小;
(2)设向量m=(cos A,cos 2A),n=(12,-5),求当m·n取最大值时,tan C的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(解析版) 题型:解答题
已知数列{an}的前三项分别为a1=5,a2=6,a3=8,且数列{an}的前n项和Sn满足Sn+m=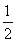 (S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(1)求数列{an}的通项公式及前n项和Sn;
(2)求满足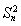 -
-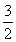 an+33=k2的所有正整数k,n.
an+33=k2的所有正整数k,n.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练A组练习卷(解析版) 题型:解答题
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB=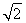 EF.
EF.
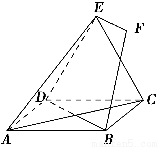
(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练F组练习卷(解析版) 题型:填空题
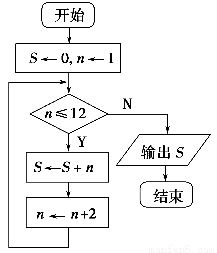
如图是一个算法的流程图,则最后输出的S=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练E组练习卷(解析版) 题型:填空题
若命题“?x∈R,使得x2+(a-1)x+1≤0”为假命题,则实数a的范围________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练B组练习卷(解析版) 题型:填空题
一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com