Question

一个多面体的直观图及三视图如图所示,其中M , N 分别是AF、BC 的中点，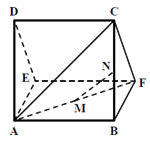
   
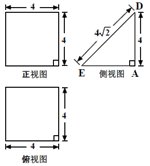
（1）求证：MN // 平面CDEF ；
（2）求二面角A-CF-B 的余弦值；

Answer 1

（1）详见解析;（2）．

解析试题分析：（1）由三视图知，该多面体是底面为直角三角形的直三棱柱ADE-BCF，且AB=BC=BF=4，DE=CF=，∠CBF=90°，由此能证明MN∥平面CDEF．（2）（法一）作BQ⊥CF于Q，连结AQ，由已知得AB⊥面BCF，AB⊥CF，BQ⊥CF，∠AQB为所求的二面角的平面角，由此能求出二面角A-CF-B的余弦值．
（2）（法二）：以EA，AB，AD所在直线为x轴，y轴，z轴，建立空间直角坐标系，利用向量法能求出二面角A-CF-B的余弦值．
试题解析：解（1）证明：由三视图知，该多面体是底面为直角三角形的直三棱柱ADE-BCF,且AB=BC=BF=4,DE=CF=,
,连结BE, M在BE上，连结CE
EM="BM,CN=BN," 所以∥,所以平面
（2）方法一：作BQ⊥CF于Q，连结AQ，
面BFC⊥面ABFE，面ABFE∩面BFC=BF，
AB?面ABFE，AB⊥BF，
∴AB⊥面BCF，
CF?面BCF，∴AB⊥CF，BQ⊥CF，AB∩BQ=B，
∴CF⊥面ABQ，AQ?面ABQ，
AQ⊥CF，∴∠AQB为所求的二面角的平面角，（8分）
在Rt△ABQ中，tan∠AQB=，
∴cos∠AQB＝，
∴二面角A-CF-B的余弦值为．
（2）方法二：以EA,AB,AD所在直线为x轴,y轴,z轴建立空间直角坐标系，

所以
面CBF法向量为

设面ACF法向量为，

取，所以
设二面角为，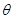
考点：1．用空间向量求平面间的夹角；2．直线与平面平行的判定．