
分析 (1)根据平面向量的数量积求模长即可;
(2)根据平面向量的数量积求向量的夹角即可.
解答 解:(1)因为|$\overrightarrow a$|=1,|$\overrightarrow b$|=2,且|$\overrightarrow a$|与|$\overrightarrow b$|的夹角为$\frac{π}{3}$,
所以$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|×|$\overrightarrow{b}$|cos$\frac{π}{3}$=1×2×$\frac{1}{2}$=1,
所以|$\overrightarrow a$+2$\overrightarrow b$|=$\sqrt{{(\overrightarrow{a}+2\overrightarrow{b})}^{2}}$
=$\sqrt{{\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+{4\overrightarrow{b}}^{2}}$
=$\sqrt{1+4×1+4×4}$
=$\sqrt{21}$;
(2)因为(2$\overrightarrow a$-$\overrightarrow{b}$)•(3$\overrightarrow a$+$\overrightarrow b$)=3,
所以(2$\overrightarrow{a}$-$\overrightarrow{b}$)•(3$\overrightarrow{a}$+$\overrightarrow{b}$)=6${\overrightarrow{a}}^{2}$-3$\overrightarrow{a}$•$\overrightarrow{b}$+2$\overrightarrow{a}$•$\overrightarrow{b}$-${\overrightarrow{b}}^{2}$
=6-$\overrightarrow{a}$•$\overrightarrow{b}$-4
=3,
解得$\overrightarrow{a}$•$\overrightarrow{b}$=-1,
设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,
则$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|×|$\overrightarrow{b}$|cosθ=1×2×cosθ=-1,
解得cosθ=-$\frac{1}{2}$;
又θ∈[0,π],
所以向量$\overrightarrow a$与$\overrightarrow b$的夹角为θ=$\frac{2π}{3}$.
点评 本题考查了利用平面向量的数量积求模长与夹角的应用问题,是基础题目.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | ($\frac{1}{7}$,$\frac{2}{7}$) | C. | ($\frac{2}{7}$,$\frac{1}{7}$) | D. | ($\frac{1}{7}$,$\frac{1}{14}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
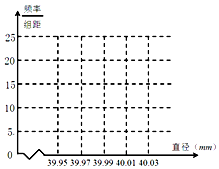 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如表频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如表频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com