练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    绝对值的几何意义

    实数a的绝对值|a|表示数轴上坐标为________的点A到________的距离．

    对于任意两个实数a，b，设它们在数轴上的对应点分别为A，B，那么|a－b|的几何意义是数轴上A，B两点之间的________，即线段AB的________．

    答案：a 原点 距离距离
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列关于复数的类比推理中，错误的是（　　）
    ①复数的加减运算可以类比多项式的加减运算；
    ②由向量
    a
    的性质|
    a
    |2=
    a
    2类比复数z的性质|z|2=z2；
    ③方程ax2+bx+c=0（a，b，c∈R）有两个不同实数根的条件是b2-4ac＞0，可以类比得到方程az2+bz+c=0（a，b，c∈C）有两个不同复数根的条件是b2-4ac＞0；
    ④由向量加法的几何意义可以类比得到复数加法的几何意义．
    A、①③B、②④C、②③D、①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

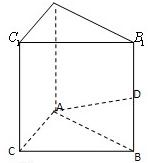    精英家教网P是平面ABCD外的点，四边形ABCD是平行四边形，
    AB
    =（2，-1，-4），
    AD
    =（4，2，0），
    AP
    =（-1，2，-1）．
    （1）求证：PA⊥平面ABCD；
    （2）对于向量
    a
    =（x1，y1z1），
    b
    =(x2y2z2)，
    c
    =(x3y3z3)    ，定义一种运算：(
    a
    ×
    b
    )•
    c
    =x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2z3-x3y2z1    ，试计算(
    AB
    ×
    AD
    )-
    AP
    的绝对值；说明其与几何体P-ABCD的体积关系，并由此猜想向量这种运算(
    AB
    ×
    AD
    )-
    AP
    的绝对值的几何意义．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    四棱锥P—ABCD中，底面ABCD是一个平行四边形，=(2，-1，-4)，=(4，2，0)，=(-1，2，-1).

    (1)求证PA⊥底面ABCD；

    (2)求四棱锥P—ABCD的体积；

    (3)对于向量a=(x1,y1,z1),b=(x2,y2,z2),c=(x3,y3,z3),定义一种运算：

    (a×b)·c=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1.

        试计算(×)·的绝对值的值；说明其与四棱锥P—ABCD体积的关系，并由此猜想向量这一运算(×)·的绝对值的几何意义.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列关于复数的类比推理中，错误的是（　　）
    ①复数的加减运算可以类比多项式的加减运算；
    ②由向量
    a
    的性质|
    a
    |2=
    a
    2类比复数z的性质|z|2=z2；
    ③方程ax2+bx+c=0（a，b，c∈R）有两个不同实数根的条件是b2-4ac＞0，可以类比得到方程az2+bz+c=0（a，b，c∈C）有两个不同复数根的条件是b2-4ac＞0；
    ④由向量加法的几何意义可以类比得到复数加法的几何意义．
    A．①③B．②④C．②③D．①④

    查看答案和解析>>

    同步练习册答案