
从{1,2,3,4,5}中随机选取一个数为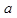 ,从{1,2,3}中随机选取一个数为
,从{1,2,3}中随机选取一个数为 ,则
,则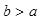 的概率是( )
的概率是( )
A. | B.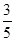 | C. | D. |
科目:高中数学 来源: 题型:单选题
下列各组事件中,不是互斥事件的是 ( )
| A.一个射手进行一次射击,命中环数大于8与命中环数小于6 |
| B.播种菜籽100粒,发芽90粒与发芽80粒 |
| C.检查某种产品,合格率高于70%与合格率为70% |
| D.统计一个班数学期中考试成绩,平均分数不低于90分与平均分数不高于120分 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列叙述错误的是( ).
A.若事件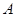 发生的概率为 发生的概率为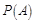 ,则 ,则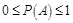 |
| B.互斥事件不一定是对立事件,但是对立事件一定是互斥事件 |
| C.5张奖券中有一张有奖,甲先抽,乙后抽,则乙与甲中奖的可能性相同 |
| D.某事件发生的概率是随着试验次数的变化而变化的 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某5个同学进行投篮比赛,已知每个同学投篮命中率为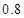 ,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记
,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记 为5个同学的得分总和,则
为5个同学的得分总和,则 的数学期望为( )
的数学期望为( )
| A.400 | B.200 | C.100 | D.80 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
盒子里有形状大小完全相同的3个红球和2个白球,如果不放回的依次取两个球,则在第一次取到白球的条件下,第二次取到红球的概率为( )
A.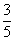 | B.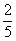 | C.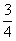 | D.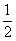 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com