已知f(x)为R上不恒为零的函数,且对于任意的a,b∈R都满足:f=af(b)+bf(a).
(1)求f(0),f(1)的值;
(2)判断f(x)的奇偶性,并证明你的结论;
(3)若f(2)=2,g(n)=f(2n)(n∈N),求g(n).
【答案】
分析:(1)根据题意,用赋值法,令a=b=0,可得f(0)的值,令a=b=1,可得f(1)=f(1)+f(1),即可得f(1);
(2)由(1)中f(1)=0的结论;再令a=b=-1,则f(1)=-2f(-1)=0,可得f(-1)的值,进而令a=x,b=-1,则f(-x)=-f(x)+xf(-1)=-f(x),即可得答案;
(3)根据题意,f(2
n)=f(2×2
n-1)=2f(2
n-1)+2
n-1f(2),又由f(2)=2,可得f(2
n)=f(2
n-1)+2
n,进而等式可以变形为

=2,则数列{f(2
n)}是首项为f(2)=2,公比为2的等比数列,由等比数列的通项公式可得答案.
解答:解:(1)根据题意,对于任意的a,b∈R都满足:f(a•b)=af(b)+bf(a),
令a=b=0,可得f(0)=0,
令a=b=1,可得f(1)=f(1)+f(1),即f(1)=0;
(2)由(1)的结论,f(1)=0;
令a=b=-1,则f(1)=-2f(-1)=0,∴f(-1)=0
令a=x,b=-1,则f(-x)=-f(x)+xf(-1)=-f(x)
f(x)为奇函数.
(3)根据题意,f(2
n)=f(2×2
n-1)=2f(2
n-1)+2
n-1f(2),
又由f(2)=2,则f(2
n)=f(2
n-1)+2
n,
等式左右两边同除2
n可得

=

,即

=2,
则数列{f(2
n)}是首项为f(2)=2,公比为2的等比数列,
则f(2
n)=2
n,
故g(n)=f(2
n)=2
n.
点评:本题考查数列与抽象函数的应用,对于抽象函数一般用赋值法,本题的难点在于将f(2
n)=f(2
n-1)+2
n,通过在等式左右两边同除2
n,得到
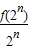
=

,由等比数列的性质来解题.

 =2,则数列{f(2n)}是首项为f(2)=2,公比为2的等比数列,由等比数列的通项公式可得答案.
=2,则数列{f(2n)}是首项为f(2)=2,公比为2的等比数列,由等比数列的通项公式可得答案. =
= ,即
,即 =2,
=2,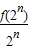 =
= ,由等比数列的性质来解题.
,由等比数列的性质来解题. 

 名校课堂系列答案
名校课堂系列答案