
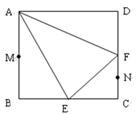
在边长为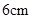 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(I)判别MN与平面AEF的位置关系,并给出证明;
(II)求多面体E-AFMN的体积.


【解析】第一问因翻折后B、C、D重合(如下图),所以MN应是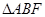 的一条中位线,则利用线线平行得到线面平行。
的一条中位线,则利用线线平行得到线面平行。
第二问因为 平面BEF,……………8分
平面BEF,……………8分
且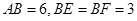 ,
,
∴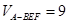 ,又
,又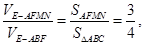 ∴
∴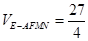
(1)因翻折后B、C、D重合(如图),

所以MN应是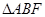 的一条中位线,………………3分
的一条中位线,………………3分
则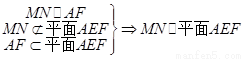 .………6分
.………6分
(2)因为 平面BEF,……………8分
平面BEF,……………8分
且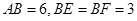 ,
,
∴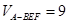 ,………………………………………10分
,………………………………………10分
又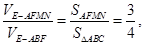 ∴
∴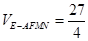
科目:高中数学 来源:2013-2014学年福建四地六校高三上学期第三次月考文科数学试卷(解析版) 题型:解答题
在边长为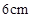 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).

(Ⅰ)在三棱锥上标注出 、
、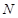 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;
(Ⅱ)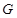 是线段
是线段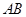 上一点,且
上一点,且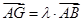 ,问是否存在点
,问是否存在点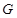 使得
使得 ,若存在,求出
,若存在,求出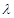 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)求多面体E-AFNM的体积.
查看答案和解析>>
科目:高中数学 来源:2014届广东省珠海市高三9月摸底考试理科数学试卷(解析版) 题型:解答题
在边长为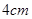 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为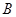 ,构成一个三棱锥.
,构成一个三棱锥.

(1)请判断 与平面
与平面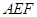 的位置关系,并给出证明;
的位置关系,并给出证明;
(2)证明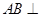 平面
平面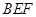 ;
;
(3)求二面角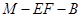 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省佛山市高三5月临考集训文科数学试卷(解析版) 题型:解答题
在边长为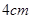 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.


(1)判别MN与平面AEF的位置关系,并给出证明;
(2)证明AB⊥平面BEF;
(3)求多面体E-AFNM的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三5月模拟考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
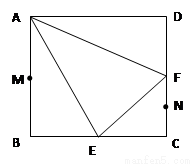
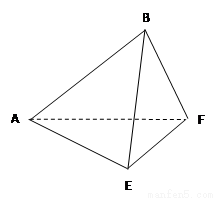
(Ⅰ)在三棱锥上标注出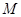 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;
(Ⅱ) 是线段
是线段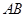 上一点,且
上一点,且 , 问是否存在点
, 问是否存在点 使得
使得 ,若存在,求出
,若存在,求出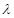 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)求多面体E-AFNM的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com