
在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC的中点.
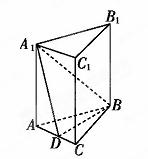
(1)求证:B1C∥平面A1BD;
(2)求平面A1DB与平面DBB1夹角的余弦值.
科目:高中数学 来源: 题型:
定义域为R的函数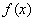 满足
满足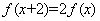 ,当
,当 [0,2)时,
[0,2)时,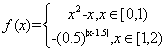 若
若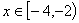 时,
时,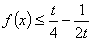 有解,则实数t的取值范围是
有解,则实数t的取值范围是
A.[-2,0)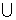 (0,l) B.[-2,0)
(0,l) B.[-2,0) 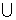 [l,+∞) C.[-2,l] D.(
[l,+∞) C.[-2,l] D.(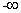 ,-2]
,-2]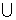 (0,l]
(0,l]
查看答案和解析>>
科目:高中数学 来源: 题型:
某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图所示,已知130~140分数段的人数为90,90~100分数段的人数为a,则下图所示程序框图的运算结果为(注:n!=1×2×3×…×n,如5!=1×2×3×4×5)
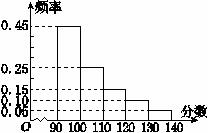

A.800! B.810! C.811! D.812!
查看答案和解析>>
科目:高中数学 来源: 题型:
某公司为了适应市场需求,对产品结构做了重大调整.调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与产量x的关系,则可选用
A.一次函数 B.二次函数 C.指数型函数 D.对数型函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com