
【题目】数列{an}和{bn}的每一项都是正数,且a1=8,b1=16,且an , bn , an+1成等差数列,bn , an+1 , bn+1成等比数列.
(1)求a2 , b2的值;
(2)求数列{an},{bn}的通项公式.
【答案】
(1)解:由2b1=a1+a2,可得a2=2b1﹣a1=24,
由 ![]() ,可得
,可得 ![]() ,
,
(2)解:∵an,bn,an+1成等差数列,故2bn=an+an+1,①
bn,an+1,bn+1成等比数列 ![]() ,
,
又数列{an}和{bn}的每一项都是正数所以 ![]() ②
②
于是,当n≥2时,有 ![]() ③
③
将②③代入①可得当n≥2时 ![]() ,
,
因此数列 ![]() 是首项为
是首项为 ![]() ,公差为2的等差数列,
,公差为2的等差数列,
∴ ![]() ,则当n≥2时,
,则当n≥2时, ![]() ,
,
当n=1时,a1=8,满足上式
【解析】(1)利用已知可得:2b1=a1+a2 , ![]() ,即可得出.(2)由已知可得:2bn=an+an+1 ,
,即可得出.(2)由已知可得:2bn=an+an+1 , ![]() ,
, ![]() ,利用递推关系可得:
,利用递推关系可得: ![]() ,利用等差数列的通项公式可得bn , 进而得到an .
,利用等差数列的通项公式可得bn , 进而得到an .
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】先后随机投掷2枚正方体骰子,其中x表示第1枚骰子出现的点数,y表示第2枚骰子出现的点数,
(1)求点P(x,y)在直线y=x﹣1上的概率;
(2)求点P(x,y)满足y2<4x的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数a∈R,函数f(x)=(a﹣x)|x|.
(1)若a=1,求f(x)的单调区间;
(2)若f(x)是奇函数,且关于x的不等式mx2+m>f[f(x)]对所有的x∈[﹣2,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x(x∈N*)名员工从事第三产业,调整后他们平均每人每年创造利润为10(a﹣ ![]() )万元(a>0),剩下的员工平均每人每年创造的利润为原来(1+
)万元(a>0),剩下的员工平均每人每年创造的利润为原来(1+ ![]() )倍.
)倍.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多可以整出多少名员工从事第三产业;
(2)若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则a的最大取值是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
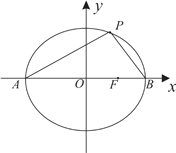
【题目】如图,已知椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,右焦点为
,右焦点为![]() ,焦距为
,焦距为![]() ,点
,点![]() 是椭圆C上异于
是椭圆C上异于![]() 两点的动点,
两点的动点, ![]() 的面积最大值为
的面积最大值为![]() .
.
(1)求椭圆C的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试判断以
,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并作出证明.
的位置关系,并作出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于![]() 分的学生进入第二阶段比赛.现有
分的学生进入第二阶段比赛.现有![]() 名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
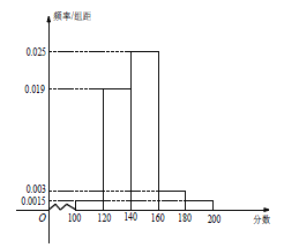
(1)估算这![]() 名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得![]() 分,进入最后强答阶段.抢答规则:抢到的队每次需猜
分,进入最后强答阶段.抢答规则:抢到的队每次需猜![]() 条谜语,猜对
条谜语,猜对![]() 条得
条得![]() 分,猜错
分,猜错![]() 条扣
条扣![]() 分.根据经验,甲队猜对每条谜语的概率均为
分.根据经验,甲队猜对每条谜语的概率均为![]() ,乙队猜对每条谜语的概率均为
,乙队猜对每条谜语的概率均为![]() ,猜对第
,猜对第![]() 条的概率均为
条的概率均为![]() .若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两条抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以2为公差,9为第五项的等差数列的第二项,则这个三角形是( )
A.锐角三角形
B.钝角三角形
C.等腰直角三角形
D.等腰或直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asin2x+bcos2x(ab≠0),有下列四个命题:其中正确命题的序号为(填上所有正确命题的序号)
①若a=1,b=﹣ ![]() ,要得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移
,要得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移 ![]() 个单位;
个单位;
②若a=1,b=﹣1,则函数y=f(x)的一个对称中心为( ![]() ,0);
,0);
③若y=f(x)的一条对称轴方程为x= ![]() ,则a=b;
,则a=b;
④若方程asin2x+bcos2x=m的正实数根从小到大依次构成一个等差数列,则这个等差数列的公差为π.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com