Question

【题目】已知函数，若存在唯一的零点，且，则的取值范围是

A. B. C. D.

Answer 1

【答案】A

【解析】当a=0时,f(x)==0,解得,函数f(x)有两个零点，不符合题意，应舍去；

当a>0时,令，,解得x=0或>0，列表如下：

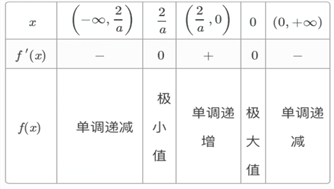
∵x→∞,f(x)→∞,而f(0)=1>0，

∴存在x<0,使得f(x)=0,不符合条件：f(x)存在唯一的零点x0,且x0>0，应舍去。

当a<0时,f′(x)=3ax26x=3ax(x)=0，,解得x=0或x=<0，列表如下：

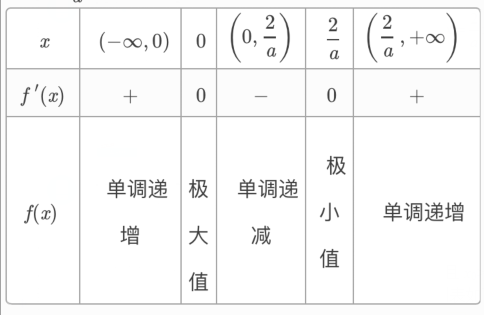
而f(0)=1>0,x→+∞时,f(x)→∞，

∴存在x0>0,使得f(x0)=0，

∵f(x)存在唯一的零点x0,且x0>0，

∴极小值f()>0,化为a2>4，

∵a<0，∴a<2.

综上可知：a的取值范围是(∞,2).

故选：A.