已知集合A={(x,y)|y≥|x-a|},B={(x,y)|y≤-a|x|+2a}(a≥0).
(1)证明A∩B≠∅;
(2)当0≤a≤4时,求由A∩B中点组成图形面积的最大值.
【答案】
分析:(1)根据(0,a)∈A,(0,2a)∈B,可得A∩B≠∅.
(2)分类讨论:当2≤a≤4时,A∩B中点组成三角形,当0<a<2时,A∩B中点组成四边形,求出相应的面积,利用导数求得面积的最大值,从而可得结论.
解答: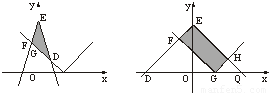
(1)证明:显然(0,a)∈A.
当x=0时,y≤-a|x|+2a=2a,
∴(0,2a)∈B.∴A∩B≠∅.
(2)解:如左上图,当2≤a≤4时,A∩B中点组成如图所示△EFD,
∴E(0,2a)、F(-
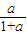
,
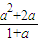
)、D(
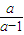
,
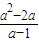
)、G(0,a).
∴S
△EFD=S
△EFG+S
△FGD=

a•
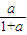
+

a•
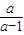
=
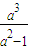
.
当0<a<2时,A∩B中点组成如右上图所示四边形EFGH.
∴E(0,2a)、F(-
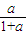
,
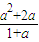
)、G(a,0)、H(
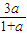
,
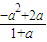
)、D(-2,0)、Q(2,0),
∴S
四边形EFGH=S
△DEQ-S
△DFG-S
△GHQ=

×4×2a-

(a+2)•
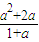
-

(2-a)•
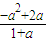
=
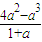
.
当a=0时,A∩B={(0,0)},显然适合上式,
∴S=
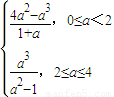
当0≤a<2时,S=

,∴S′=
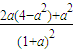
>0
∴S=
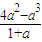
在[0,2)上是增函数.∴0≤S<

.
当a≥2时,S=
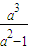
,∴S′=
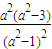
>0,
∴S=
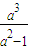
在[2,4]上是增函数,∴

≤S≤
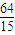
.
综上所述,当a=4时,A∩B中点组成图形面积取得最大值
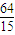
.
点评:本题考查A∩B中点组成图形面积的计算,考查利用导数求最大值,考查分类讨论的数学思想,属于中档题.

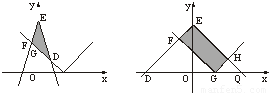 (1)证明:显然(0,a)∈A.
(1)证明:显然(0,a)∈A.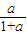 ,
,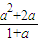 )、D(
)、D(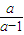 ,
,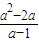 )、G(0,a).
)、G(0,a). a•
a•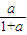 +
+ a•
a•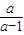 =
=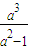 .
.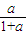 ,
,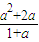 )、G(a,0)、H(
)、G(a,0)、H(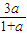 ,
,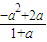 )、D(-2,0)、Q(2,0),
)、D(-2,0)、Q(2,0), ×4×2a-
×4×2a- (a+2)•
(a+2)•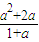 -
- (2-a)•
(2-a)•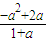 =
=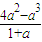 .
.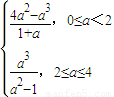
 ,∴S′=
,∴S′=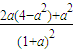 >0
>0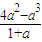 在[0,2)上是增函数.∴0≤S<
在[0,2)上是增函数.∴0≤S< .
.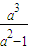 ,∴S′=
,∴S′=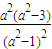 >0,
>0,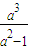 在[2,4]上是增函数,∴
在[2,4]上是增函数,∴ ≤S≤
≤S≤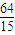 .
.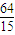 .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案