在一个给定的正(2n+1)边形的顶点中随机地选取三个不同的顶点,任何一种选法的可能性是相等的,则正多边形的中心位于所选三个点构成的三角形内部的概率为 .
【答案】
分析:从(2n+1)边形的顶点中随机地选取三个不同的顶点中取3个的所有不同的取法有C
2n+13,每种取法等可能出现,属于古典概率,正多边形的中心位于所选三个点构成的三角形内部,若第一个点取的就是点2n+1,对于第二个点分类考虑:第二个点取取的是点1,第二个点取的是点2…第二个点取的是m,第二个点取的是点n,再考虑第三个点的所有取法,利用古典概率的公式可求.
解答:解:不妨设以时钟12点方向的顶点为点2n+1,顺时针方向的下一个点为点1,则以时钟12点和6点连线为轴,左右两边各有n个点.
多边形中心位于三角形内部的三角形个数a:
假设第一个点取的就是点2n+1,则剩下的两点必然在轴线的一左一右.
对于第二个点取的是点1,
对于第二个点取的是点2,第三个点能取点n+1、点n+2,有2种
…
对于第二个点取的是点m,第三个点能取点n+1、点n+2…点n+m,有m种
…
对于第二个点取的是点n,第三个点能取点n+1,点n+2…点2n,有n种
一共1+2+…n=

(n+1)n种
如果第二个点取的是点n+1到点2n,可视为上述情况中的第三个点.
所以a=

(n+1)n×

(2n+1)=

(2n+1)(n+1)n
一共可构成三角形个数b=

(2n+1)n(2n-1)
∴P=
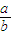
=
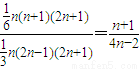
故答案为:
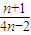 点评:
点评:本题主要考查了等可能事件的概率公式的应用,解题的关键是求解基本事件的个数时要合理的分类,灵活利用组合数,本题有一定的难度.

 (n+1)n种
(n+1)n种 (n+1)n×
(n+1)n× (2n+1)=
(2n+1)= (2n+1)(n+1)n
(2n+1)(n+1)n (2n+1)n(2n-1)
(2n+1)n(2n-1)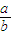 =
=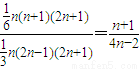
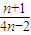


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案