练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    对于函数f(x)＝－x4＋x3＋ax2－2x－2，其中a为实常数，已知函数

    y＝f(x)的图象在点(－1，f(－1))处的切线与y轴垂直．

    (Ⅰ)求实数a的值；

    (Ⅱ)若关于x的方程f(3x)＝m有三个不等实根，求实数m的取值范围；

    答案：
    解析：

    　　解：(Ⅰ)．

    　　据题意，当时取极值，所以．

    　　因为．

    　　由1－2a＝0，得．　6分

    　　(Ⅱ)因为，则．

    　　所以．

    　　由，得，即x＜－1或1＜x＜2．

    　　所以f(x)在区间，(1，2)上单调递增，

    　　在区间(－1，1)，(2，＋∞)上单调递减．　8分

    　　所以的极大值为，

    　　极小值为．　11分

    　　由此可得函数y＝f(x)的大致图象如下：

    　　令，若关于的方程有三个不等实根，

    　　则关于的方程在上有三个不等实根，

    　　即函数的图象与直线在上有三个不同的交点．

    　　又，由图象可知，，

    　　故的取值范围是．　15分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    “我们称使f(x)＝0的x为函数y＝f(x)的零点．若函数y＝f(x)在区间[a，b]上是连续的、单调的函数，且满足f(a)·f(b)<0，则函数y＝f(x)在区间[a，b]上有唯一的零点”．对于函数f(x)＝6ln(x＋1)－x2＋2x－1.

    (1)讨论函数f(x)在其定义域内的单调性，并求出函数极值；

    (2)证明连续函数f(x)在[2，＋∞)内只有一个零点．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省高三第四次月考文科数学试卷（解析版） 题型：解答题

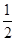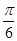    本小题满分12分）  对于函数f(x)＝(asin x＋cos x)cos x－，已知f()=1．

    (1)求a的值； 

    (2)作出函数f(x)在x∈[0，π]上的图像(不要求书写作图过程)．

    (3)根据画出的图象写出函数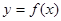在上的单调区间和最值.

     

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学必修一3.1函数与方程练习卷（一）（解析版） 题型：填空题

    下列说法正确的有________：

    ①对于函数f(x)＝x2＋mx＋n，若f(a)＞0，f(b)＞0，则函数f(x)在区间(a，b)内一定没有零点．

    ②函数f(x)＝2x－x2有两个零点．

    ③若奇函数、偶函数有零点，其和为0.

    ④当a＝1时，函数f(x)＝|x2－2x|－a有三个零点．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年安徽省高三第四次质量检测文科数学试卷 题型：填空题

    对于函数f(x)＝2cos2x＋2sinxcosx－1(x∈R)给出下列命题：①f(x)的最小正周期为2π；②f(x)在区间[，]上是减函数；③直线x＝是f(x)的图像的一条对称轴；④f(x)的图像可以由函数y＝sin2x的图像向左平移而得到．其中正确命题的序号是________(把你认为正确的都填上)

     

    查看答案和解析>>

    同步练习册答案