当向量a=c=.b=(1.0)时.执行如图所示的程序框图.输出的i值为( ) A.5B.4C.3D.2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

当向量

=c=（-2，2），

=（1，0）时，执行如图所示的程序框图，输出的i值为（　　）

A、5

B、4

C、3

D、2

考点：程序框图

专题：算法和程序框图

分析：模拟程序运行，依次写出每次循环得到的

的值，当

=（-2，2），满足条件a•c=0，退出循环，输出i的值为4．

解答： 解：模拟程序运行，有
i=1时，

=（-1，2），不满足条件a•c=0
i=2时，

=（0，2），不满足条件a•c=0
i=3时，

=（1，2），不满足条件a•c=0
i=4时，

=（-2，2），满足条件a•c=0
退出循环，输出i的值为4．
故选：B．

点评：本题主要考察了程序框图和算法，正确理解循环结构的功能是解题的关键，属于基本知识的考查．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

过点P（3，1）作圆C：（x-2）²+y²=1的两条切线，切点分别为A、B，则直线AB的方程为（　　）

A、x+y-3=0

B、x-y-3=0

C、2x-y-3=0

D、2x+y-3=0

查看答案和解析>>

科目：高中数学 来源： 题型：

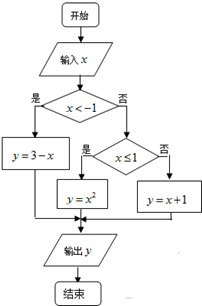阅读右边的算法流程图（如图），解答下列问题：
（1）写出算法输出的结果y=f（x）；
（2）已知命题p：{x|f（x）≤1}；命题q：关于x的不等式x²-3ax+2a²＞0（a＞0）的解集，且q是p的必要不充分条件，求a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

已知f（x）=

(3-a)x，x∈(-∞，1]

ax，x∈(1，+∞)

是（-∞，+∞）上的增函数，那么实数a的取值范围是（　　）

A、（0，3）

B、（1，3）

C、（1，+∞）

D、[

，3)

查看答案和解析>>

科目：高中数学 来源： 题型：

某市现有居民300万人，每天有1%的人选择乘出租车出行，记每个人的乘车里程为x（km），1≤x≤21．由调查数据得到x的频率分布直方图（如图），在直方图的乘车里程分组中，可以用各组在区间中点值代表该组的各个值，乘车里程落入该区间的频率作为乘车里程取该区间中点值的概率，现规定乘车里程x≤3时，乘车费用为10元；当x＞3时，每超出1km（不足1km时按1km计算），乘车费用增加1.3元．
（Ⅰ）求从乘客中任选2人乘车里程超过10km的概率；
（Ⅱ）试估计出租车公司一天的总收入是多少？（精确到0.01万元）

查看答案和解析>>

科目：高中数学 来源： 题型：

已知向量

=（sinx，2

sinx），

=（2cosx，sinx），定义f（x）=

•

（1）求函数y=f（x），x∈R的单调递减区间；
（2）若函数y=f（x+θ）（0＜θ＜

）为偶函数，求θ的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

已知线段PQ的两个端点的坐标分别为P（-1，6）、Q（2，2），若直线mx+y-m=0与线段PQ有交点，则实数m的取值范围是（　　）