解:(I)由

∥

,可得3sinx=-cosx,于是tanx=-

.
∴
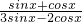
=
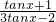
=
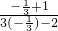
=-

.
(II)∵在△ABC中,A+B=π-C,于是sin(A+B)=sinC,
由

c=2asin(A+B)利用正弦定理得:

sinC=2sinAsinC,
∴sinA=

,可解得 A=

. …(6分)
又△ABC为锐角三角形,于是

<B<

,
∵函数f(x)=(

+

)•

=(sinx+cosx,2)•(sinx,-1)
=sin
2x+sinxcosx-2=

+

-2=

sin(2x-

)-

.
∴f(B+

)=

sin[2(B+

)-

]-

=

sin2B-

.…(10分)
由

<B<

得

<2B<π,
∴0<sin2B≤1,得-

<

sin2B-

≤

-

,即 f(B+

)的取值范围 (-

,

-

].
分析:(I)由

∥

,可得tanx=-

,再由
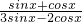
=
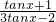
,运算求得结果.
(II)在△ABC中,由

c=2asin(A+B)利用正弦定理求得sinA=

,可解得 A=

.由△ABC为锐角三角形,得

<B<

,利用两个向量的数量积公式求得函数f(x)=

sin(2x-

)-

.由此可得f(B+

)=

sin2B-

,再根据B的范围求出sin2B的范围,即可求得f(B+

)的取值范围.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦定理,正弦函数的定义域和值域,两个向量的数量积公式的应用,属于中档题.

 =(sinx,-1),
=(sinx,-1), =(cosx,3).
=(cosx,3). ∥
∥ 时,求
时,求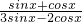 的值;
的值; c=2asin(A+B),函数f(x)=(
c=2asin(A+B),函数f(x)=( +
+ )•
)• ,求f(B+
,求f(B+ )的取值范围.
)的取值范围. ∥
∥ ,可得3sinx=-cosx,于是tanx=-
,可得3sinx=-cosx,于是tanx=- .
.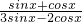 =
=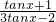 =
=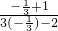 =-
=- .
.  c=2asin(A+B)利用正弦定理得:
c=2asin(A+B)利用正弦定理得: sinC=2sinAsinC,
sinC=2sinAsinC, ,可解得 A=
,可解得 A= . …(6分)
. …(6分) <B<
<B< ,
, +
+ )•
)• =(sinx+cosx,2)•(sinx,-1)
=(sinx+cosx,2)•(sinx,-1) +
+ -2=
-2= sin(2x-
sin(2x- )-
)- .
. )=
)= sin[2(B+
sin[2(B+ )-
)- ]-
]- =
= sin2B-
sin2B- .…(10分)
.…(10分) <B<
<B< 得
得 <2B<π,
<2B<π, <
< sin2B-
sin2B- ≤
≤ -
- ,即 f(B+
,即 f(B+ )的取值范围 (-
)的取值范围 (- ,
, -
- ].
]. ∥
∥ ,可得tanx=-
,可得tanx=- ,再由
,再由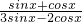 =
=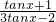 ,运算求得结果.
,运算求得结果. c=2asin(A+B)利用正弦定理求得sinA=
c=2asin(A+B)利用正弦定理求得sinA= ,可解得 A=
,可解得 A= .由△ABC为锐角三角形,得
.由△ABC为锐角三角形,得 <B<
<B< ,利用两个向量的数量积公式求得函数f(x)=
,利用两个向量的数量积公式求得函数f(x)= sin(2x-
sin(2x- )-
)- .由此可得f(B+
.由此可得f(B+ )=
)= sin2B-
sin2B- ,再根据B的范围求出sin2B的范围,即可求得f(B+
,再根据B的范围求出sin2B的范围,即可求得f(B+ )的取值范围.
)的取值范围.

 阅读快车系列答案
阅读快车系列答案