已知Sn为等差数列{an}的前n项和,且a3=S3=9
(Ⅰ)求{an}的通项公式;
(Ⅱ)若等比数列{bn}满足b1=a2,b4=S4,求{bn}的前n项和公式.
解:(Ⅰ)设等差数列{a
n}的公差为d.
因为a
3=S
3=9,
所以
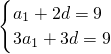
,解得a
1=-3,d=6,
所以a
n=-3+(n-1)•6=6n-9;
(II)设等比数列{b
n}的公比为q,
因为b
1=a
2=-3+6=3,b
4=S
4=4×(-3)+

=24,
所以3q
3=24,解得q=2,
所以{b
n}的前n项和公式为

=3(2
n-1).
分析:(Ⅰ)设等差数列{a
n}的公差为d,由a
3=S
3=9,得
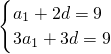
,解出a
1,d,由等差数列通项公式即可求得答案;
(Ⅱ)设等比数列{b
n}的公比为q,由b
1=a
2可得b
1,由b
4=S
4可得q,由等比数列前n项和公式可得答案;
点评:本题考查等差数列的通项公式及等比数列的前n项和公式,通项公式、前n项和公式是解决等差、等比数列的基础,应熟练掌握.

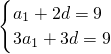 ,解得a1=-3,d=6,
,解得a1=-3,d=6, =24,
=24, =3(2n-1).
=3(2n-1).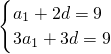 ,解出a1,d,由等差数列通项公式即可求得答案;
,解出a1,d,由等差数列通项公式即可求得答案;
