
(本小题满分12分)
在 中,
中,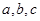 分别为内角
分别为内角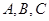 的对边,且
的对边,且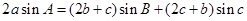 .
.
(1)求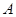
 的大小;
的大小;
(2)若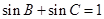 ,试判断
,试判断 的形状;
的形状;
(1) 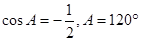 . (2)
. (2)  是等腰的钝角三角形.
是等腰的钝角三角形.
解析试题分析:(Ⅰ)利用正弦定理把题设等式中的角的正弦转化成边,求得a,b和c关系式,代入余弦定理中求得cosA的值,进而求得A.
(Ⅱ)把(Ⅰ)中a,b和c关系式利用正弦定理转化成角的正弦,与sinB+sinC=1联立求得sinB和sinC的值,进而根据C,B的范围推断出B=C,可知△ABC是等腰的钝角三角形
(1)由已知,根据正弦定理得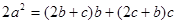 ,
,
即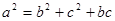 .
.
由余弦定理得 ,
,
故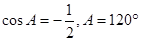 .……6分
.……6分
(2)由(1)得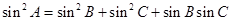 .
.
又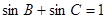 ,得
,得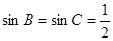 .
.
因为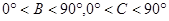 ,
,
故B=C.
所以 是等腰的钝角三角形. …………12分考点:本题主要考查正弦定理和余弦定理的应用.
是等腰的钝角三角形. …………12分考点:本题主要考查正弦定理和余弦定理的应用.
点评:解决该试题的关键是在解三角形问题中一般借助正弦定理和余弦定理边化角,角化边达到解题的目的.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(本题满分13 分)
据气象部门预报,在距离某码头南偏东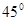 方向600km处的热带风暴中心,正以每小时20km的速度向正北方向移动,距风暴中心450km以内的地区都将受到影响,从现在起多长时间后,该码头将受到热带风暴中心的影响,影响多长时间?(精确到0.1h)
方向600km处的热带风暴中心,正以每小时20km的速度向正北方向移动,距风暴中心450km以内的地区都将受到影响,从现在起多长时间后,该码头将受到热带风暴中心的影响,影响多长时间?(精确到0.1h)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知CD=6 ,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, 是佛山市一环东线的一段,其中
是佛山市一环东线的一段,其中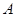 、
、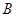 、
、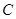 分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界
分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界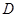 位于点
位于点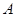 的北偏东
的北偏东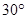 方向
方向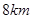 处,位于点
处,位于点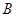 的正北方向,位于点
的正北方向,位于点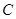 的北偏西
的北偏西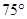 方向上,并且
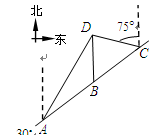
方向上,并且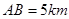 .
.
(1) 求佛陈路出口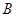 与花卉世界
与花卉世界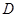 之间的距离;(精确到0.1km)
之间的距离;(精确到0.1km)
(2) 求花卉大道出口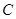 与花卉世界
与花卉世界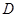 之间的距离.(精确到0.1km)
之间的距离.(精确到0.1km)
(参考数据: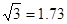 ,
,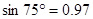 ,
,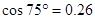 ,
,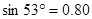 ,
,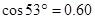 ,
, 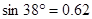 ,
,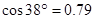
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com