练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知a和b是两条异面直线, A和B是a上不同的两点, C和D是b上不同的两点, E、F分别是线段AC和BD的中点. 那么EF和AB, EF和CD的关系是

    [　　]

    A. 两对异面直线.　　　　　　   B.三条交于一点的直线.

    C.一对平行, 一对异面的直线.　　D.以上都不对

    答案：A
    解析：

    解：

    如图, 假定直线EF和AB共面, 设此平面为N. 由a和b是异面直线, 知道C与A是不同的点, 因而AC的中点E与A点不重合. 直线AC上有两个不同的点A和E在平面N内,因而直线AC上所有各点都在平面N内C点当然在平面N内,同理D点也在平面N内.直线b上有不同的两点C和D在平面N内, 因而直线b在平面N内. 这样一来, 直线b和a就要在同一平面N内. 而已知a和b是异面直线, 出现矛盾. 所以EF和AB是异面直线. 同理EF和CD是异面直线.


    提示：

    用实例观察


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013届黑龙江省大庆铁人中学高三第三次阶段理科数学试卷（带解析） 题型：填空题

    下列四个命题：
    ①直线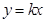与圆恒有公共点；
    ②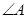为△ABC的内角，则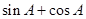最小值为；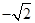
    ③已知a，b是两条异面直线，则过空间任意一点P都能作并且只能作一条直线与a，b都垂直；
    ④等差数列{}中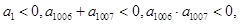，则使其前n项和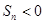成立的最大正整数为2013;
    其中正确命题的序号为               。（将你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2013届山西省太原市第五中学高三4月月考文科数学试卷（带解析） 题型：填空题

    下列四个命题：
    ①直线与圆恒有公共点；
    ②为△ABC的内角，则最小值为；
    ③已知a，b是两条异面直线，则过空间任意一点P都能作并且只能作一条直线与a，b都垂直；
    ④等差数列{}中，则使其前n项和成立的最大正整数为2013;
    其中正确命题的序号为           。（将你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山西省太原市高三4月月考文科数学试卷（解析版） 题型：填空题

    下列四个命题：

    ①直线与圆恒有公共点；

    ②为△ABC的内角，则最小值为；

    ③已知a，b是两条异面直线，则过空间任意一点P都能作并且只能作一条直线与a，b都垂直；

    ④等差数列{}中，则使其前n项和成立的最大正整数为2013;

    其中正确命题的序号为           。（将你认为正确的命题的序号都填上）

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年黑龙江省高三第三次阶段理科数学试卷（解析版） 题型：填空题

    下列四个命题：

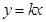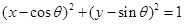    ①直线与圆恒有公共点；

    ②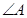为△ABC的内角，则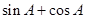最小值为；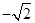

    ③已知a，b是两条异面直线，则过空间任意一点P都能作并且只能作一条直线与a，b都垂直；

    ④等差数列{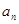}中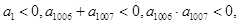，则使其前n项和成立的最大正整数为2013;

    其中正确命题的序号为               。（将你认为正确的命题的序号都填上）

     

    查看答案和解析>>

    同步练习册答案