练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

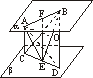
    如图，两异面线段AB、CD分别在两平行平面α、β内，α、β间的距离为h，若三棱锥A－BCD是侧棱与底棱均相等的正三棱锥，则其体积为

    [　　]
    A．

    B．

    h3

    C．

    D．

    答案：C
    解析：

    解：∵ABα，CDβ，且α∥β，∴AB与CD间的距离为h．取CD的中点E，连结AE、BE，则CD⊥面AEB．过E作EF⊥AB，则EF＝h．设正四面体棱长为a，则在△AEF中，h2＝(a)2－()2，得h＝a，即a＝h，过A作AO⊥BE，则AO⊥面BCD，在Rt△AOE中，求得AO＝a，∴VA－BCD＝·a2·a＝．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

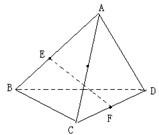    精英家教网如图，在四面体ABCD中，已知所有棱长都为a，点E、F分别是AB、CD的中点．
    （1）求线段EF的长；（EF是两异面直线AB与CD的公垂线）；
    （2）求异面直线BC、AD所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源：湖南石门一中2007届高三第二次月考理科数学试卷 题型：013

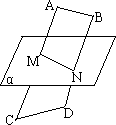
    如图，两异面直线AB、CD都平行于平面α，M、N分别为AC、BD的中点，且M∈α，N∈α设线段AB＋CD＝l，则有

    [　　]

    A．MN＞l

    B．MN＜l

    C．MN＝l

    D．三种情况都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：

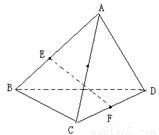
    如图，在四面体ABCD中，已知所有棱长都为a，点E、F分别是AB、CD的中点.

    （1）求线段EF的长;(EF是两异面直线AB与CD的公垂线)；     

    （2）求异面直线BC、AD所成角的大小.１２分

     

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年黑龙江省鹤岗一中高一（下）期末数学试卷（理科）（解析版） 题型：解答题

    如图，在四面体ABCD中，已知所有棱长都为a，点E、F分别是AB、CD的中点．
    （1）求线段EF的长；（EF是两异面直线AB与CD的公垂线）；
    （2）求异面直线BC、AD所成角的大小．

    查看答案和解析>>

    同步练习册答案