
| 80 | 1-r% |
| 80 |
| 1-r% |
| 80 |
| 1-r% |
| 80 |
| 1-r% |
| 80 |
| 1-r% |
| 80(8-0.62r)r |
| 100-r |
| 400 |
| 31 |
| 400 |
| 31 |
| 80(8-0.62r)r |
| 100-r |
| 100 |
| 31 |
| 100 |
| 31 |


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
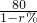 元才能保证公司利润,由于提价每年将少销售0.62r万件.
元才能保证公司利润,由于提价每年将少销售0.62r万件.查看答案和解析>>
科目:高中数学 来源: 题型:
某服装公司生产的衬衫,每件定价80元,在某城年销售8万件.现该公司在该市设立代理商来销售衬衫.代理商要收取代销费,代销费为销售金额的![]() (即每销售100元收取
(即每销售100元收取![]() 元).为此,该衬衫每件价格要提高到
元).为此,该衬衫每件价格要提高到![]() 元才能保证公司利润,由于提价每年将少销售
元才能保证公司利润,由于提价每年将少销售![]() 万件.
万件.
(1)试将代理商收取的年代理费![]() 表示为
表示为![]() 的函数;
的函数;
(2)如果代理商每年收取的代理费不小于16万元,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 80 |
| 1-r% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com