
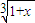 ,x∈[1,2],证明:φ(x)∈A;
,x∈[1,2],证明:φ(x)∈A;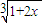 单调增的性质,得x∈[1,2]时1<
单调增的性质,得x∈[1,2]时1<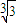 ≤φ(2x)≤
≤φ(2x)≤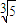 <2,从而得到φ(2x)∈(1,2);再根据分子有理化,整理得|φ(2x1)-φ(2x2)|=|x1-x2|•
<2,从而得到φ(2x)∈(1,2);再根据分子有理化,整理得|φ(2x1)-φ(2x2)|=|x1-x2|•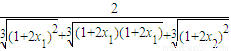 ,从而令
,从而令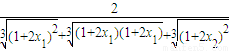 =L,得0<L<1满足|φ(2x1)-φ(2x2)|≤L|x1-x2|.由以上两条可得φ(x)∈A成立;
=L,得0<L<1满足|φ(2x1)-φ(2x2)|≤L|x1-x2|.由以上两条可得φ(x)∈A成立; ∈(1,2)且x≠
∈(1,2)且x≠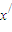 ,使得x=φ(2x),
,使得x=φ(2x),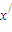 =φ(2
=φ(2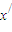 ),根据(I)的结论进行推理得到|x-
),根据(I)的结论进行推理得到|x-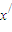 |≤L|x1-x2|,所以L≥1与定义0<L<1矛盾,从而说明假设不成立,可得满足x∈(1,2)且x=φ(2x)的x是唯一的.
|≤L|x1-x2|,所以L≥1与定义0<L<1矛盾,从而说明假设不成立,可得满足x∈(1,2)且x=φ(2x)的x是唯一的.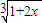 ,
,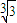 ≤φ(2x)≤
≤φ(2x)≤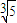 ,且1<
,且1<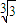 <
<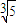 <2,
<2,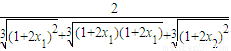 ,
,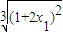 +
+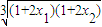 +
+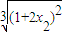 ,
,
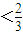 ,
, =L,则0<L<1,
=L,则0<L<1,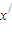 ∈(1,2)且x≠
∈(1,2)且x≠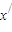 ,使得x=φ(2x),
,使得x=φ(2x),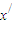 =φ(2
=φ(2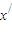 ),则
),则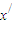 )|≤L|x1-x2|,
)|≤L|x1-x2|,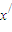 |≤L|x1-x2|,所以L≥1,与定义0<L<1矛盾,故假设不成立,
|≤L|x1-x2|,所以L≥1,与定义0<L<1矛盾,故假设不成立,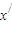 ∈(1,2)且x≠
∈(1,2)且x≠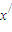 ,使得x=φ(2x),
,使得x=φ(2x),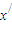 =φ(2
=φ(2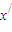 ),
),

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
| 3 | 1+x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 1+x |
| Lk-1 |
| 1-L |
查看答案和解析>>
科目:高中数学 来源:延庆县一模 题型:解答题
| 3 | 1+x |
查看答案和解析>>
科目:高中数学 来源:延庆县一模 题型:解答题
| 3 | 1+x |
| Lk-1 |
| 1-L |
查看答案和解析>>
科目:高中数学 来源: 题型:
A是由定义在[2,4]上且满足如下条件的函数![]() (x)组成的集合:①对任意的
(x)组成的集合:①对任意的![]() 都有
都有![]() (2x)
(2x)![]() ;②存在常数L(0<L<1),使得对任意的x1,x2
;②存在常数L(0<L<1),使得对任意的x1,x2![]() [1,2],都有|
[1,2],都有|![]() (2x1)-
(2x1)-![]() (2 x2)|
(2 x2)|![]() .
.
(Ⅰ)设![]() (x)=
(x)=![]() 证明:
证明:![]() (x)
(x)![]() A:
A:
(Ⅱ)设![]() (x)
(x)![]() ,如果存在x0
,如果存在x0![]() (1,2),使得x0=
(1,2),使得x0=![]() (2x0),那么这样的x0是唯一的:
(2x0),那么这样的x0是唯一的:
(Ⅲ)设![]()
![]() 任取x1
任取x1![]() (1,2),令xn+1=
(1,2),令xn+1=![]() (2xn),n=1,2……证明:给定正整数k,对任意的正整数p,成立不等式
(2xn),n=1,2……证明:给定正整数k,对任意的正整数p,成立不等式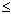 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com