练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20.

    A是由定义在[2，4]上且满足如下条件的函数（x）组成的集合：①对任意的都有(2x);②存在常数L（0＜L＜1），使得对任意的x1,x2[1，2]，都有|（2x1）- (2 x2)|.

    （Ⅰ）设（x）=证明：（x）A:

    （Ⅱ）设（x），如果存在x0(1,2),使得x0=（2x0）,那么这样的x0是唯一的：

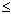    （Ⅲ）设任取x1(1,2),令xn+1=（2xn）,n=1,2……证明：给定正整数k，对任意的正整数p,成立不等式Equation.3。

    解（Ⅰ）由题设，对任意

           ∵

           又∵对任意的

        

     

    而

    ∴

    令，显然存在常数L(0＜L＜1),

    使得

    综上所述，可知

    （Ⅱ）（运用反证法证明）

         设存在两个实数。

         因为则由

    ∴L≥1，这与题设矛盾，从而所证命题结论成立。

    （Ⅲ）因为

    ∴

                （其中0＜L＜1）

    ∴

                      

                       Equation.3

     

    故∴对于给定正整数k，对任意的正整数p不等式均成立

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•延庆县一模）A是由定义在[2，4]上且满足如下条件的函数φ（x）组成的集合：
    （1）对任意x∈[1，2]，都有φ（2x）∈（1，2）；
    （2）存在常数L（0＜L＜1），使得对任意的x1，x2∈[1，2]，都有|φ（2x1）-φ（2x2）|≤L|x1-x2|．
    （Ⅰ）设φ（x）=
    31+x
    ，x∈[1，2]，证明：φ（x）∈A；
    （Ⅱ）设φ（x）∈A，如果存在x0∈（1，2），使得x0=φ（2x0），那么这样的x0是唯一的．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•延庆县一模）A是由定义在[2，4]上且满足如下条件的函数φ（x）组成的集合：
    （1）对任意x∈[1，2]，都有φ（2x）∈（1，2）；
    （2）存在常数L（0＜L＜0），使得对任意的x1，x2∈[1，2]，都有|?（2x1）-?（2x2）|≤L|x1-x2|．
    （Ⅰ）设φ（x）=
    31+x
    ，x∈[2，4]，证明：φ（x）∈A；
    （Ⅱ）设φ（x）∈A，如果存在x0∈（1，2），使得x0=φ（2x0），那么这样的x0是唯一的；
    （Ⅲ）设φ（x）∈A，任取xn∈（1，2），令xn+1=φ（2nx），n=1，2，…，证明：给定正整数k，对任意的正整数p，不等式|xk+p-xk|≤
    Lk-1
    1-L
    |x2-x1|    成立．

    查看答案和解析>>

    科目：高中数学 来源：延庆县一模 题型：解答题

    A是由定义在[2，4]上且满足如下条件的函数φ（x）组成的集合：
    （1）对任意x∈[1，2]，都有φ（2x）∈（1，2）；
    （2）存在常数L（0＜L＜0），使得对任意的x1，x2∈[1，2]，都有|?（2x1）-?（2x2）|≤L|x1-x2|．
    （Ⅰ）设φ（x）=
    31+x
    ，x∈[2，4]，证明：φ（x）∈A；
    （Ⅱ）设φ（x）∈A，如果存在x0∈（1，2），使得x0=φ（2x0），那么这样的x0是唯一的；
    （Ⅲ）设φ（x）∈A，任取xn∈（1，2），令xn+1=φ（2nx），n=1，2，…，证明：给定正整数k，对任意的正整数p，不等式|xk+p-xk|≤
    Lk-1
    1-L
    |x2-x1|    成立．

    查看答案和解析>>

    科目：高中数学 来源：广东省高考真题 题型：证明题

    A是由定义在[2，4]上且满足如下条件的函数φ（x）组成的集合：
    ①对任意x∈[1，2]，都有φ（2x）∈（1，2） ；
    ②存在常数L（0＜L＜1），使得对任意的x1，x2∈[1，2]，都有|φ（2x1）-φ（2x2）|≤L|x1-x2|，
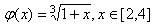    （Ⅰ）设，证明：φ（x）∈A；
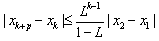    （Ⅱ）设φ（x）∈A，如果存在x0∈（1，2），使得x0=φ（2x0），那么这样的x0是唯一的；
    （Ⅲ）设φ（x）∈A，任取x1∈（1，2），令xn+1=φ（2xn），n=1，2，…，证明：给定正整数k，对任意的正整数p，成立不等式。

    查看答案和解析>>

    同步练习册答案