
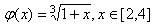 ��֤�����գ�x����A��
��֤�����գ�x����A��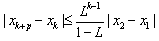 ��
�� ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 | 1+x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 | 1+x |
| Lk-1 |
| 1-L |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������һģ ���ͣ������
| 3 | 1+x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������һģ ���ͣ������
| 3 | 1+x |
| Lk-1 |
| 1-L |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
A���ɶ�����[2��4]�����������������ĺ���![]() ��x����ɵļ��ϣ��ٶ������
��x����ɵļ��ϣ��ٶ������![]() ����
����![]() (2x)
(2x)![]() ;�ڴ��ڳ���L��0��L��1����ʹ�ö������x1,x2
;�ڴ��ڳ���L��0��L��1����ʹ�ö������x1,x2![]() [1��2]������|
[1��2]������|![]() ��2x1��-
��2x1��-![]() (2 x2)|
(2 x2)|![]() .
.
������![]() ��x��=
��x��=![]() ֤����
֤����![]() ��x��
��x��![]() A:
A:
������![]() ��x��
��x��![]() ���������x0
���������x0![]() (1,2),ʹ��x0=
(1,2),ʹ��x0=![]() ��2x0��,��ô������x0��Ψһ�ģ�
��2x0��,��ô������x0��Ψһ�ģ�
������![]()
![]() ��ȡx1
��ȡx1![]() (1,2),��xn+1=
(1,2),��xn+1=![]() ��2xn��,n=1,2����֤��������������k���������������p,��������ʽ
��2xn��,n=1,2����֤��������������k���������������p,��������ʽ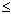 ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com