练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知椭圆C的方程为+=1,试确定m的取值范围，使得对一直线y=4x+m,椭圆C上有不同两点P、Q关于该直线对称.

    思路解析：本题解法很多，可以由Δ判定，也可以由交轨法，还可以考虑设而不求.

    解法一：设出对称的两点的坐标及其所在的直线方程，再利用判别式Δ＞0及中心在对称轴上来求解.

    设椭圆C上关于直线l对称的两点为P（x1,y1）、Q(x2,y2),其所在直线方程为y=-x+b,代入椭圆方程3x2+4y2=12,整理得13x2-8bx+16b2-48=0.

    ∵x1≠x2,∴Δ=-192(4b2-13)＞0,解得-＜b＜.                          ①

    又∵=,=-,+b=b,

    而点（,）在直线y=4x+m上，

    ∴m=-4·=-b.∴b=-m.                                     ②

    将②代入①可解得-＜m＜,

    即所求m的范围内（-,）.

    解法二：根据中点M必在P、Q两点之间，建立不等式，将问题转化为求解直线y=4x+m和过P、Q两点所在的直线的交点问题.

    设PQ中点坐标为M（x0,y0）.

    由解法一知，2x0=x1+x2=,x1x2=,

    由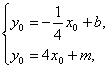消去y0，把x0=b代入可得m=-b,∴x0=-m.

    由于中点M的位置（介于P、Q）之间必有不等关系（x1-x0）(x2-x0)＜0,由此可得-＜m＜.

    经验证，当-＜m＜时，

    -＜b＜.

    适合条件的点P、Q存在.

    ∴-＜m＜.

    解法三：联想与弦的中点有关，利用“设而不求”法，可转化为利用均值不等式求出m的范围.

    设P(x1,y1),Q(x2,y2),

    若P、Q关于直线l:y=4x+m对称，当且仅当下列条件组成立.

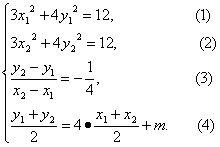
    （1）-（2）并把（3）代入,得y1+y2=3(x1+x2).                                              （5）

    把（5）代入（4）,得x1+x2=-2m.                                                            （6）

    把（6）代入（5）,得y1+y2=-6m.                                                             （7）

    ①+②,得3（x12+x22）+4(y12+y22)=24.                                       （8）

    由题意x1≠x2,y1≠y2,根据均值不等式有

    x12+x22＞,y12+y22＞.

    ∴3(x12+x22)+4(y12+y22)＞ (x1+x2)2+2(y1+y2)2.                 （9）

    把（6）（7）（8）代入（9），解得-＜m＜,

    即m∈(-,).

    解法四：C上存在不同的两点关于直线l对称，等价于存在C的弦被l垂直平分，且垂足必在椭圆C的内部，因此，这类问题可转化为利用交点在曲线C内部建立不等式.

    设P(x1,y1),Q(x2,y2),PQ中点M（x0,y0），代入椭圆方程有

    3x12+4y12=12,           ①       3x22+4y22=12,           ②

    ①-②得=-=-=-.                    ③

    又y0=4x0+m,                                                                 ④

    由③④解得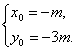

    ∵M(-m,-3m)在椭圆的内部，

    ∴3（-m）2+4(-3m)2＜12,解得-＜m＜.

    即m∈(-,).

    解法五：利用C上存在不同的两点P、Q关于直线l对称，则线段PQ中点必在l上，也必在椭圆C的斜率为-的平行弦的中点轨迹上，把问题整体转化为求椭圆C的斜率为-的平行弦中点的轨迹与直线l交点在椭圆C内部时的参数的取值范围问题.

    设A(x1,y1)、B(x2,y2)是椭圆上的点，且kAB=-,M(x,y)是AB的中点，则有

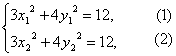
    （1）-（2）,得3（x1-x2）(x1+x2)+4(y1-y2)(y1+y2)=0.

    ∴3x+4y=0,即3x+4y·(-)=0,∴y=3x.

    ∴椭圆C的斜率为-的平行弦中点轨迹是y=3x在椭圆C内的部分.

    由得交点（-m,-3m）.

    ∵交点在椭圆C内，∴3（-m）2+4(-3m)2＜12.

    解得-＜m＜.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆C的方程为
    x2
    a2
    +
    y2
    b2
    =1(a≥2b＞0)    ．
    （1）求椭圆C的离心率的取值范围；
    （2）若椭圆C与椭圆2x2+5y2=50有相同的焦点，且过点M（4，1），求椭圆C的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C的方程为
    x2
    a2
    + 
    y2
    b2
    =1    （a＞b＞0），称圆心在坐标原点O，半径为
    		a2+b2
    的圆为椭圆C的“伴随圆”，椭圆C的短轴长为2，离心率为
    		6
    3
    ．
    （Ⅰ）求椭圆C及其“伴随圆”的方程；
    （Ⅱ）若直线l与椭圆C交于A，B两点，与其“伴随圆”交于C，D两点，当|CD|=
    		13
     时，求△AOB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•泉州模拟）已知椭圆C的方程为：
    x2
    a2
    +
    y2
    2
    =1 (a＞0)    ，其焦点在x轴上，离心率e=
    		2
    2
    ．
    （1）求该椭圆的标准方程；
    （2）设动点P（x0，y0）满足
    OP
    =
    OM
    +2
    ON
    ，其中M，N是椭圆C上的点，直线OM与ON的斜率之积为-
    1
    2
    ，求证：x02+2
    y
    2
    0
    为定值．
    （3）在（2）的条件下，问：是否存在两个定点A，B，使得|PA|+|PB|为定值？若存在，给出证明；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•衡阳模拟）已知椭圆C的方程为
    y2
    a2
    +
    x2
    b2
    =1（a＞b＞0），离心率e=
    		2
    2
    ，上焦点到直线y=
    a2
    c
    的距离为
    		2
    2
    ，直线l与y轴交于一点P（0，m），与椭圆C交于相异两点A，B且
    AP
    =t
    PB
    ．
    （1）求椭圆C的方程；
    （2）若
    OA
    +t
    OB
    =4
    OP
    ，求m的取值范围•

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C的方程为
    x 2
    4
    +
    y2
    3
    =1，过C的右焦点F的直线与C相交于A、B两点，向量
    m
    =(-1，-4)，若向量
    OA
    -
    OB
    与
    m
    -
    OF
    共线，则直线AB的方程是（　　）

    查看答案和解析>>

    同步练习册答案