
(本题12分)为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
|
小麦产量 |
|
|
|
|
|
|
频数 |
10 |
35 |
40 |
10 |
5 |
表2:不施用新化肥小麦产量频数分布表
|
小麦产量 |
|
|
|
|
|
频数 |
15 |
50 |
30 |
5 |
(10) 完成下面频率分布直方图;

(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量;
(3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3:
|
|
小麦产量小于20kg |
小麦产量不小于20kg |
合计 |
|
施用新化肥 |
|
|
|
|
不施用新化肥 |
|
|
|
|
合计 |
|
|
|
附:
|
|
0.050 |
0.010 |
0.005 |
0.001 |
|
|
3.841 |
6.635 |
7.879 |
10.828 |
(1)见解析; (2) 施用化肥的平均产量为21.5,不施用新化肥的平均产量为17.5; (3)列量表见解析,99.5%。
【解析】
试题分析:
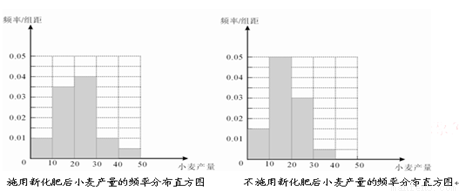 4分
4分
(2)施用化肥的一小块土地小麦平均产量为
5×0.1+15×0.35+25×0.4+35×0.1+45×0.05=21.5 ………6分
不施用新化肥的一小块土地小麦平均产量为
5×0.15+15×0.5+25×0.3+35×0.05=17.5 ………8分
(3)表3
|
|
小麦产量小于20kg |
小麦产量不小于20kg |
合计 |
|
施用新化肥 |
|
|
100 |
|
不施用新化肥 |
|
|
100 |
|
合计 |
110 |
90[来源:] |
|
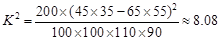 ………11分
………11分
由于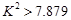 ,所以有99.5%的把握认为施用新化肥和不施用新化肥的小麦产量有差异
………12分
,所以有99.5%的把握认为施用新化肥和不施用新化肥的小麦产量有差异
………12分
考点:频率分布直方图;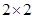 列联表;独立性检验。
列联表;独立性检验。
点评:在频率分布直方图中:小长方形的面积=组距× =频率,各个长方形的面积之和等于1。属于基础题。
=频率,各个长方形的面积之和等于1。属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2010-2011年黑龙江省牡丹江一中高二上学期期末考试数学理卷 题型:解答题
(本小题满分12分)
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图如下图所示,已知后6组的频数从左到右依次是等差数列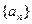 的
的 前六项。
前六项。
(1)试确定视力介于4.9至5.0的抽查学生的人数。
(2)若规定视力低于5.0的学生属于近视 学生,试估计该校新生的近视率
学生,试估计该校新生的近视率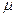 的大
的大
小。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省湛江市高三下学期第六次月考考试文科数学 题型:解答题
.(本题12分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
, ,
, ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?

查看答案和解析>>
科目:高中数学 来源:2010-2011学年吉林省高三第一次模拟考试文科数学卷 题型:解答题
(本小题满分12分)
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列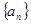 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列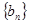 的前六项.
的前六项.
(I)求等比数列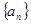 的通项公式;
的通项公式;
(II)求等差数列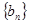 的通项公式;
的通项公式;
(III)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率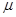 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源:2010-2011年黑龙江省高二上学期期末考试数学理卷 题型:解答题
(本小题满分12分)
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图如下图所示,已知后6组的频数从左到右依次是等差数列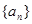 的前六项。
的前六项。
(1)试确定视力介于4.9至5.0的抽查学生的人数。
(2)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率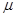 的大
的大
小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com