练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

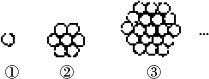
    如下图，①，②，③，…是由花盆摆成的图形，根据图中花盆摆放的规律，第n个图形中的花盆数an＝________．

    (提示：n＋(n＋1)＋…＋(2n－2)＋(2n－1)＋(2n－2)＋…＋(n＋1)＋n＝3n2－3n＋1)．

    答案：
    解析：

    　　答案　3n2－3n＋1

    　　解：仔细观察发现：

    　　图形①的花盆数为1，a1＝1；

    　　图形②的花盆中间一行的个数为3，上下两行都是2个，a2＝2＋3＋2；

    　　图形③的花盆中间一行的个数为5，上面两行由下到上分别递减1个，且关于中间一行上下对称，a3＝3＋4＋5＋4＋3；…

    　　可以猜想：第n个图形中的花盆中间数为2n－1，上面每行由下到上分别递减1个，最上面有n个，且关于中间行上下对称，因此an＝n＋(n＋1)＋…＋(2n－2)＋(2n－1)＋(2n－2)＋…＋(n＋1)＋n＝3n2－3n＋1．

    　　点评：由归纳推理所得的结论虽然未必是可靠的，但通过观察，对有限的资料作归纳整理，找出规律是解决这类题的基本方法．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在如下图所示的程序框图中，当程序被执行后，输出s的结果是
     
    ．
    精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在集合{a，b，c，d}上定义两种运算⊕和?（如下图），则d?（a⊕c）=
    a
    a
    ．
    ? a b c d
     a a a a a
    b a b c d
    c a c c a
    d a d a d
    ⊕ a b c d
    a a b c d
    b b b b b
    c c b c b
    d d b b d

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=Asin（ωx+?）（A＞0，ω＞0，|?|＜
    π2
    ）在一个周期内的图象如下图所示．
    （1）求函数的解析式；
    （2）求函数的单调递增区间；
    （3）设0＜x＜π，且方程f（x）=m有两个不同的实数根，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    甲、乙两名运动员的5次测试成绩如下图所示设s1，s2分别表示甲、乙两名运动员测试成绩的标准差，
    .
    x1
    ，
    .
    x2
    分别表示甲、乙两名运动员测试成绩的平均数，则有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图所示，两射线OA与OB交于点O，下列5个向量中，
    ①2
    OA
    -
    OB
      ②
    3
    4
    OA
    +
    1
    3
    OB
     ③
    1
    2
    OA
    +
    1
    3
    OB
     ④
    3
    4
    OA
    +
    1
    5
    OB
      ⑤
    3
    4
    OA
    -
    1
    5
    OB

    若以O为起点，终点落在阴影区域内（含边界）的向量有（　　）个．

    查看答案和解析>>

    同步练习册答案