练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设f(x)=x2-x+14,且|x-a|<1,求证:|f(x)-f(a)|<2(|a|+1).


     由题知

    |f(x)-f(a)|=|x2-a2+a-x|=|(x-a)(x+a-1)|=|x-a||x+a-1|<|x+a-1|=|(x-a)+2a-1|≤|x-a|+|2a|+1<|2a|+2=2(|a|+1),即得证.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设a＞b＞1，c＜0，给出下列三个结论：

       ①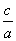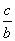＞；②ac＜bc；③logb(a－c)＞loga(b－c)．

    其中所有的正确结论的序号是(　　)

    A．①     B．①②     C．②③     D．①②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若对任意x＞0，≤a恒成立，则a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数 ，则不等式的解集为                .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某花店每天以每枝元的价格从农场购进若干枝玫瑰花，然后以每枝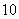元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理.

    （Ⅰ）若花店一天购进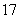枝玫瑰花，求当天的利润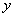（单位：元）关于当天需求量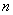（单位：枝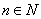，）的函数解析式；

    （Ⅱ）花店记录了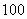天玫瑰花的日需求量（单位：枝），整理得下表：

    日需求量

    频数

    ① 假设花店在这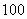天内每天购进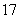枝玫瑰花，求这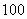天的日利润（单位：元）的平均数；

    ② 若花店一天购进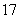枝玫瑰花，以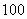天记录的的各需求量的频率作为各需求量发生的概率，求当天的利润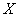（单位：元）的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知|x|<1,|y|<1,求证:|1-xy|>|x-y|.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知双曲线C：－＝1(a>0，b>0)的离心率为，则C的渐近线方程为(　　)

    A．y＝±x             B．y＝±x   C．y＝±x             D．y＝±x

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两点A(3,2)和B(－1,4)到直线mx＋y＋3＝0的距离相等，则m的值为(　　)

    A．0或－              B.或－6

    C．－或              D．0或

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    双曲线－＝1的离心率为， 则m＝__________.

    查看答案和解析>>

    同步练习册答案