
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得到如下数据:
之间的关系,经过调查得到如下数据:
间隔时间( | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数( | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.
的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.
(1)若选取的是后面4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断(1)中的方程是否是“恰当回归方程”;
(3)为了使等候的乘客不超过35人,试用(1)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: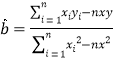
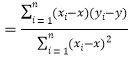 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】曲线C是平面内与两个定点![]() ,
,![]() 的距离之积等于常数
的距离之积等于常数![]() 的点的轨迹,给出下列三个结论:
的点的轨迹,给出下列三个结论:
①曲线过坐标原点;②曲线关于坐标原点对称;
③曲线关于横轴对称;④曲线关于纵轴对称;
⑤曲线关于![]() 对称;⑥若点P在曲线上,则
对称;⑥若点P在曲线上,则![]() 的面积不大于
的面积不大于![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.该原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图,在空间直角坐标系中的![]() 平面内,若函数
平面内,若函数![]() 的图象与
的图象与![]() 轴围成一个封闭的区域
轴围成一个封闭的区域![]() ,将区域
,将区域![]() 沿
沿![]() 轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域![]() 的面积相等,则此圆柱的体积为__________.
的面积相等,则此圆柱的体积为__________.
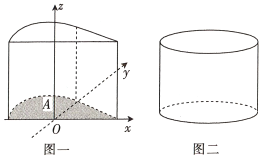
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径、圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.
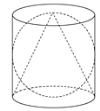
(1)试计算出图案中球与圆柱的体积比;
(2)假设球半径![]() .试计算出图案中圆锥的体积和表面积.
.试计算出图案中圆锥的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司年初以200万元购进一艘轮船,以每年40万元的价格出租给海运公司.轮船公司负责轮船的维护,第一年维护费为4万元,随着轮船的使用与磨损,以后每年的维护费比上一年多2万元,同时该轮船第![]() 年末可以以
年末可以以![]() 万元的价格出售.
万元的价格出售.
(1)写出轮船公司到第![]() 年末所得总利润
年末所得总利润![]() 万元关于
万元关于![]() 的函数解析式,并求
的函数解析式,并求![]() 的最大值;
的最大值;
(2)为使轮船公司年平均利润最大,轮船公司应在第几年末出售轮船?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,左焦点
的中心在原点,左焦点![]() 、右焦点
、右焦点![]() 都在
都在![]() 轴上,点
轴上,点![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为
的面积的最大值为![]() ,在
,在![]() 轴上方使
轴上方使![]() 成立的点
成立的点![]() 只有一个.
只有一个.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的两直线
的两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,
,![]() 和点
和点![]() ,
,![]() ,且
,且![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() ,点
,点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交椭圆
的直线交椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
①若直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
②设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,是否存在定点
,是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() 与点
与点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 过定点
过定点![]() ,且斜率为
,且斜率为![]() ,若椭圆
,若椭圆![]() 上存在
上存在![]() ,
,![]() 两点关于直线
两点关于直线![]() 对称,
对称,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围及
的取值范围及![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com