
 (n=1,2,…)
(n=1,2,…) ,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an.
,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an. 代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值,把n=4及a4的值代入已知的等式即可求出a5的值,然后把求出的五项的值变形后,即可归纳总结得到这个数列的通项公式an.
代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值,把n=4及a4的值代入已知的等式即可求出a5的值,然后把求出的五项的值变形后,即可归纳总结得到这个数列的通项公式an.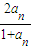 =an,解得an=0或1.
=an,解得an=0或1. ,得到a2=
,得到a2= =
= =
= ,
,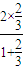 =
=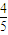 =
=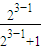 ,
,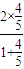 =
= =
=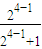 ,
, =
=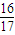 =
=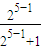 ,
, (n∈N*).
(n∈N*).

科目:高中数学 来源: 题型:
| 2an |
| 1+an |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2an |
| 1+an |
| 1 |
| 2 |
| an+P |
| an |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2an |
| 1+an |
| 1 |
| 2 |
| an+P |
| an |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年福建省宁德市霞浦一中高二(下)第一次月考数学试卷(文科)(实验班)(解析版) 题型:解答题
 (n=1,2,…)
(n=1,2,…) ,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an;
,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an; 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com