
|
| y | 2 n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| an+1 | ||
(n+1
|
| an | ||
|
| 1 | ||
|
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| an |
| n2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
(n-1
|
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| y | 2 n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
(n-1
|
| an |
| n2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
(n-1
|
| an+1 |
| (n+1)2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| an+1 | ||
(n+1
|
| an | ||
|
| 1 | ||
|
| 1 |
| a1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 5 |
| 2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1+an | ||
|
| n2 | ||
(n+1
|
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1+a1 |
| a1 |
| 1+a2 |
| a2 |
| 1+a3 |
| a3 |
| 1+an |
| an |
| 1+a1 |
| a1 |
| 1 |
| a2 |
| 1+a2 |
| a3 |
| 1+a3 |
| a4 |
| 1+an-1 |
| an |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| n-1 |
| n |
| n |
| n+1 |
| 2an+1 |
| (n+1)2 |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 1ΓΝ2 |
| 1 |
| 2ΓΝ3 |
| 1 |
| (n-1)ΓΝn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |


 ΩΈΧΟΝΖΦ”≤βœΒΝ–¥πΑΗ
ΩΈΧΟΝΖΦ”≤βœΒΝ–¥πΑΗ «αΥ…ΩΈΧΟΒΞ‘Σ≤β ‘ABΨμœΒΝ–¥πΑΗ
«αΥ…ΩΈΧΟΒΞ‘Σ≤β ‘ABΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
|
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
…ηnΓ N*Θ§≤ΜΒ» ΫΉι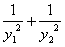 Υυ±μ ΨΒΡΤΫΟφ«χ”ρΈΣDnΘ§Α―DnΡΎΒΡ’ϊΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΘ©Α¥ΤδΒΫ‘≠ΒψΒΡΨύάκ¥”ΫϋΒΫ‘Ε≈≈Ν–≥…ΒψΝ–ΘΚ(x1,y1),(x2,y2),Γ≠,(xn,yn).
Υυ±μ ΨΒΡΤΫΟφ«χ”ρΈΣDnΘ§Α―DnΡΎΒΡ’ϊΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΘ©Α¥ΤδΒΫ‘≠ΒψΒΡΨύάκ¥”ΫϋΒΫ‘Ε≈≈Ν–≥…ΒψΝ–ΘΚ(x1,y1),(x2,y2),Γ≠,(xn,yn).
Θ®1Θ©«σ(xn,yn)ΘΜ
Θ®2Θ©…η ΐΝ–{an}¬ζΉψa1=x1,an=yn2(![]() +
+![]() +Γ≠+
+Γ≠+![]() )(nΓί2),«σ÷ΛΘΚnΓί2 ±Θ§
)(nΓί2),«σ÷ΛΘΚnΓί2 ±Θ§![]() ΘΜ
ΘΜ
Θ®3Θ©‘ΎΘ®2aΘ©ΒΡΧθΦΰœ¬Θ§±»Ϋœ(1+![]() )(1+
)(1+![]() )Γ≠(1+
)Γ≠(1+![]() )”κ4ΒΡ¥σ–Γ.
)”κ4ΒΡ¥σ–Γ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ2012-2013―ßΡξΧλΫρ“Μ÷–ΗΏ»ΐΘ®œ¬Θ©ΒΎΕΰ¥Έ‘¬ΩΦ ΐ―ß ‘ΨμΘ®άμΩΤΘ©Θ®ΫβΈωΑφΘ© Χβ–ΆΘΚΫβ¥πΧβ
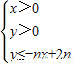 Υυ±μ ΨΒΡΤΫΟφ«χ”ρΈΣDnΘ§Α―DnΡΎΒΡ’ϊΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΘ©Α¥ΤδΒΫ‘≠ΒψΒΡΨύάκ¥”ΫϋΒΫ‘Ε≈≈Ν–≥…ΒψΝ–ΘΚΘ®x1Θ§y1Θ©Θ§Θ®x2Θ§y2Θ©Θ§Γ≠Θ§Θ®xnΘ§ynΘ©
Υυ±μ ΨΒΡΤΫΟφ«χ”ρΈΣDnΘ§Α―DnΡΎΒΡ’ϊΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΘ©Α¥ΤδΒΫ‘≠ΒψΒΡΨύάκ¥”ΫϋΒΫ‘Ε≈≈Ν–≥…ΒψΝ–ΘΚΘ®x1Θ§y1Θ©Θ§Θ®x2Θ§y2Θ©Θ§Γ≠Θ§Θ®xnΘ§ynΘ©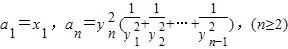 Θ§«σ÷ΛΘΚnΓί2 ±Θ§
Θ§«σ÷ΛΘΚnΓί2 ±Θ§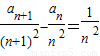 ΘΜ
ΘΜ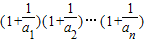 ”κ4ΒΡ¥σ–ΓΘ°
”κ4ΒΡ¥σ–ΓΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ2007-2008―ßΡξ’ψΫ≠ ΓΈ¬÷ί –ΑΥ–ΘΝΣΩΦΗΏ»ΐΘ®…œΘ©ΤΎΡ© ΐ―ß ‘ΨμΘ®άμΩΤΘ©Θ®ΫβΈωΑφΘ© Χβ–ΆΘΚΫβ¥πΧβ
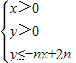 Υυ±μ ΨΒΡΤΫΟφ«χ”ρΈΣDnΘ§Α―DnΡΎΒΡ’ϊΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΘ©Α¥ΤδΒΫ‘≠ΒψΒΡΨύάκ¥”ΫϋΒΫ‘Ε≈≈Ν–≥…ΒψΝ–ΘΚΘ®x1Θ§y1Θ©Θ§Θ®x2Θ§y2Θ©Θ§Γ≠Θ§Θ®xnΘ§ynΘ©
Υυ±μ ΨΒΡΤΫΟφ«χ”ρΈΣDnΘ§Α―DnΡΎΒΡ’ϊΒψΘ®ΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΒΡΒψΘ©Α¥ΤδΒΫ‘≠ΒψΒΡΨύάκ¥”ΫϋΒΫ‘Ε≈≈Ν–≥…ΒψΝ–ΘΚΘ®x1Θ§y1Θ©Θ§Θ®x2Θ§y2Θ©Θ§Γ≠Θ§Θ®xnΘ§ynΘ©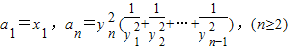 Θ§«σ÷ΛΘΚnΓί2 ±Θ§
Θ§«σ÷ΛΘΚnΓί2 ±Θ§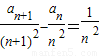 ΘΜ
ΘΜ ”κ4ΒΡ¥σ–ΓΘ°
”κ4ΒΡ¥σ–ΓΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com