
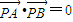 .
.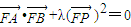 恒成立,求λ的值.
恒成立,求λ的值.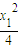 ),由此推导出直线PA的方程是:y=
),由此推导出直线PA的方程是:y=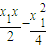 .同理,直线PB的方程是:y=
.同理,直线PB的方程是:y=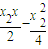 .由此能求出y.
.由此能求出y.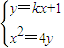 ,得x2-4kx-4b=0,由此能够证明直线AB恒过定点.
,得x2-4kx-4b=0,由此能够证明直线AB恒过定点.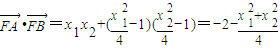 (
(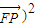 +2,能推导出存在λ=1,使得
+2,能推导出存在λ=1,使得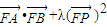 =0.
=0.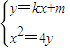 ,得到直线PA的方程是:y=kx-k2.同理可得直线PB的方程是:y=-
,得到直线PA的方程是:y=kx-k2.同理可得直线PB的方程是:y=-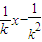 .由此能求y.
.由此能求y.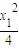 ),由x2=4y,得:y′=
),由x2=4y,得:y′=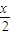 ,故kPA=
,故kPA=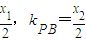 ,由
,由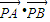 =0,知x1x2=-4.设直线AB为y=kx+1,联立
=0,知x1x2=-4.设直线AB为y=kx+1,联立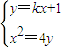 ,得x2-4kx-4b=0,由此能够证明直线AB恒过定点.
,得x2-4kx-4b=0,由此能够证明直线AB恒过定点.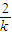 ,
,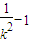 ),知
),知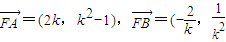 -1),
-1),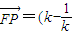 ,-2),由此能推导出存在λ=1使得
,-2),由此能推导出存在λ=1使得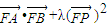 =0.
=0.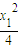 ),
),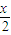 ,∴kPA=
,∴kPA=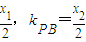 ∵
∵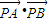 =0,
=0,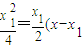 )即y=
)即y=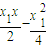 ①
①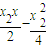 ②,(4分)
②,(4分)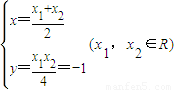
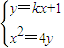 ,得x2-4kx-4b=0,
,得x2-4kx-4b=0,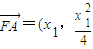 -1),
-1),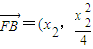 -1),P(
-1),P(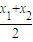 ,-1)
,-1)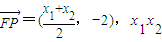 =-4,
=-4, (
(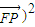 +2,
+2,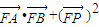 =0
=0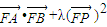 =0.(14分)
=0.(14分)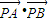 =0,
=0,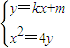 得:x2-4kx-4m=0.(2分)
得:x2-4kx-4m=0.(2分)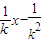 ,(4分)
,(4分)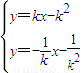 得:
得: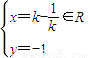 ,
, ),
),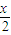 ,∴kPA=
,∴kPA=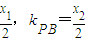 ,∵
,∵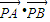 =0,
=0,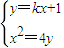 ,得x2-4kx-4b=0,
,得x2-4kx-4b=0,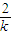 ,
,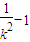 ),
),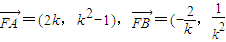 -1),
-1),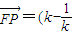 ,-2)
,-2)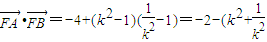 ).
).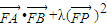 =0.(14分)
=0.(14分)

 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
| PA |
| PB |
| FA |
| FB |
| FP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PA |
| PB |
| FA |
| FB |
| FP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PA |
| PB |
| FA |
| FB |
| FP |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| PA |
| PB |
| FA |
| FB |
| FP |
查看答案和解析>>
科目:高中数学 来源:2011年福建省南平市高三适应性考试数学试卷(文科)(解析版) 题型:解答题
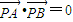 .
.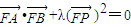 ?若存在,求出λ的值,若不存在,请说明理由.
?若存在,求出λ的值,若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com