
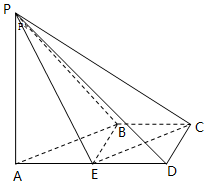
 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,异面直线PA与CD所成的角为90°. 分析 (Ⅰ)由已知异面直线PA与CD所成的角为90°,知PA⊥CD,又∠ADC=90°,直接利用线面垂直的判定可得CD⊥平面PAD;
(Ⅱ)由(Ⅰ)知∠PDA为二面角P-CD-A的平面角为45°,再由线面垂直的判定证明PA⊥平面ABCD,得PA⊥AD.证明四边形BCDE为正方形,然后利用等积法求得几何体C-PBE的体积.
解答 (Ⅰ)证明:由已知异面直线PA与CD所成的角为90°,知PA⊥CD,
又∠ADC=90°,PA∩AD=A,
∴CD⊥平面PAD;
(Ⅱ)解:由(Ⅰ)知,CD⊥平面PAD,
∴PD⊥DC,又AD⊥DC,
∴∠PDA为二面角P-CD-A的平面角为45°,
∵$\frac{1}{2}$AD=1,∴AD=2,
由PA⊥CD,∠PAB=90°,且直线AB与CD相交,
可得PA⊥平面ABCD,得PA⊥AD.
在Rt△PAD中,可得PA=2,
又AD∥BC,AD⊥DC,BC=CD,
∴四边形BCDE为正方形,可得${S}_{△BCE}=\frac{1}{2}$.
∴${V}_{C-PBE}={V}_{P-BCE}=\frac{1}{3}×\frac{1}{2}×2=\frac{1}{3}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{6}$,-2) | B. | ($\frac{π}{12}$,2) | C. | ($-\frac{π}{12}$,-2) | D. | ($-\frac{π}{12}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | -20 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x-y-4=0 | B. | 4x+y-4=0 | C. | 4x+y+4=0 | D. | 4x-y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,-2),r=2 | B. | (1,-2),$r=\sqrt{2}$ | C. | (-1,2),r=2 | D. | (-1,2),$r=\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (9,49) | B. | (13,49) | C. | (9,25) | D. | (3,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com