练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

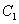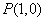    已知椭圆：的右顶点为，过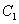的焦点且垂直长轴的弦长为．

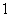    （I）求椭圆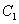的方程；

    （II）设抛物线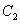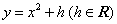：的焦点为F，过F点的直线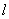交抛物线与A、B两点，过A、B两点分别作抛物线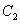的切线交于Q点，且Q点在椭圆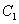上，求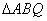面积的最值，并求出取得最值时的抛物线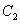的方程。


    解：（I）由题意得所求的椭圆方程为

    （II）令  

    设切线AQ方程为代入令可得

    抛物线在点A处的切线斜率为

    所以切线AQ方程为:

    同理可得BQ方程为:

    联立解得Q点为

    焦点F坐标为(0, ), 令l方程为:  代入：

    得:      由韦达定理有：

    所以Q点为

    过Q作y轴平行线交AB于M点， 则

    M点为, 

    ,

     -而Q点在椭圆上,


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知集合A={ (x，y)|x，y为实数，且x2+y2=l}，B={(x，y) |x，y为实数，且y=x}，  则A ∩ B的子集个数为_______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知恒过定点(1,1)的圆C截直线所得弦长为2，则圆心C的轨迹方程为      .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设、分别为具有公共焦点、的椭圆和双曲线的离心率，是两曲线的一个公共点，且满足,则的值为

        A.            B.2               C.            D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


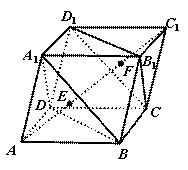
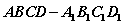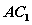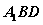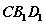    已知平行六面体，与平面，交于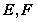两点。给出以下命题，其中真命题有______(写出所有正确命题的序号)

    ①点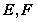为线段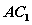的两个三等分点；

    ②；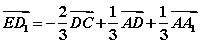

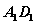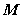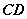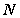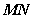    ③设中点为，的中点为，则直线与面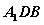有一个交点；

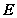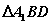    ④为的内心；

    ⑤若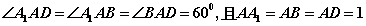,则三棱锥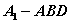为正三棱锥，且.

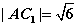    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知为等差数列，其前项和为．若，，，则      ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设是双曲线的两个焦点，是上一点，若，且的最小内角为，则的渐近线方程为      ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在四边形ABCD中，设=a，b，=c，则=(  )

        (A)-a+b+c      (B)-a+b-c    (C)a+b+c       (D)a-b+c

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    右图是函数在一个周期内的图象，此函数的解析式为可为(    )

     A．       B．

    C．      ) D．

    查看答案和解析>>

    同步练习册答案