练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．从个位数与十位数之和为奇数的两位数中任取一个，其中个位数为0的概率是$\frac{1}{9}$．

    分析 先求个位数与十位数之和为奇数的两位数的个数n，然后再求个位数与十位数之和为奇数的两位数的个数，由古典概率的求解公式可求．

    解答 解：个位数与十位数之和为奇数的两位数中，其个位数与十位数有一个为奇数，一个为偶数，共有C51C51+C51C41=45
    记：“个位数与十位数之和为奇数的两位数中，其个位数为0”为事件A，则A包含的结果：10，30，50，70，90共5个
    由古典概率的求解公式可得，P（A）=$\frac{5}{45}$=$\frac{1}{9}$．
    故答案为：$\frac{1}{9}$．

    点评 本题主要考查了古典概率的求解公式的应用，解题的关键是灵活利用简单的排列、组合的知识求解基本事件的个数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F作一条渐近线l的平行线交双曲线C于A，若以A为圆心，2a为半径的圆与l相切，则双曲线C的离心率e的值为$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．动直线x=m（m＞0）与函数f（x）=2x+$\frac{1}{x}$，g（x）=x-$\frac{1}{x}$-lnx分别交于点A，B，则|AB|的最小值为（　　）
    A．3+ln2B．2C．$\frac{7}{2}$-ln2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知双曲线C：$\frac{{x}^{2}}{m+3}$-$\frac{{y}^{2}}{m}$=1（m＞0）的渐近线方程为y=±$\frac{1}{2}$x，则双曲线C的焦距为（　　）
    A．1B．2$\sqrt{5}$C．3D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

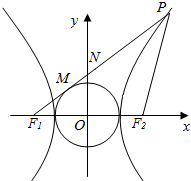    18．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，P为双曲线右支上一点，直线PF1与圆x2+y2=a2相切，且|PF2|=|F1F2|，则该双曲线的离心率e是$\frac{5}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．${（\sqrt{7}-1）^0}-{（\frac{16}{9}）^{-\;\frac{1}{2}}}-{2^{{{log}_2}\frac{1}{3}}}•{log_2}\frac{1}{8}$的值为$\frac{5}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

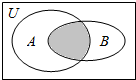
    15．（文）设全集U=R，集合A={x|x2+4x＜0}，集合B={x|x＜-2}，则图中阴影部分表示的集合为（　　）
    A．{x|-4＜x＜-2}B．{x|-4＜x＜0}C．{x|x＞0}D．{x|x＜-2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若抛物线C的焦点是双曲线16x2-9y2=144的左焦点，则抛物线C的标准方程为y2=-20x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知a＞0，且a≠1，求使方程loga（x-ak）=loga$\sqrt{{x}^{2}-{a}^{2}}$有解的k的取值范围．

    查看答案和解析>>

    同步练习册答案