
 A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y};
A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}; ,
,
| 解:(Ⅰ)集合组1具有性质P, 所对应的数表为:
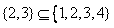 , ,有  , ,与对任意的 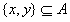 ,都至少存在一个i∈{1,2,3},有 ,都至少存在一个i∈{1,2,3},有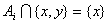 或{y}矛盾, 或{y}矛盾,所以集合组 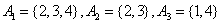 不具有性质P。 不具有性质P。(Ⅱ)
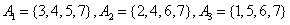 ; ;(注:表格中的7行可以交换得到不同的表格,它们所对应的集合组也不同) (Ⅲ)设 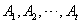 所对应的数表为数表M, 所对应的数表为数表M,因为集合组 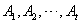 为具有性质P的集合组,所以集合组 为具有性质P的集合组,所以集合组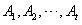 满足条件①和②, 满足条件①和②,由条件①: 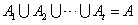 , ,可得对任意x∈A,都存在i∈{1,2,3,…,t}有 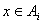 , ,所以 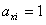 ,即第x行不全为0, ,即第x行不全为0,所以由条件①可知数表M中任意一行不全为0; 由条件②知,对任意的 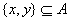 ,都至少存在一个i∈{1,2,3,…,t}, ,都至少存在一个i∈{1,2,3,…,t},使 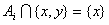 或{y}, 或{y},所以 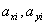 一定是一个1一个0,即第x行与第y行的第i列的两个数一定不同; 一定是一个1一个0,即第x行与第y行的第i列的两个数一定不同;所以由条件②可得数表M中任意两行不完全相同; 因为由0,1所构成的t元有序数组共有2t个,去掉全是0的t元有序数组,共有 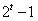 个, 个,又因数表M中任意两行都不完全相同,所以 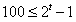 ,所以t≥7, ,所以t≥7,又t=7时,由0,1所构成的7元有序数组共有128个,去掉全是0的数组,共127个, 选择其中的100个数组构造100行7列数表,则数表对应的集合组满足条件①②,即具有性质P,所以t=7; 因为 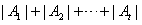 等于表格中数字1的个数, 等于表格中数字1的个数,所以,要使 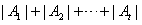 取得最小值,只需使表中1的个数尽可能少, 取得最小值,只需使表中1的个数尽可能少,而t=7时,在数表M中, 1的个数为1的行最多7行; 1的个数为2的行最多 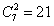 行; 行;1的个数为3的行最多 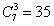 行; 行;1的个数为4的行最多 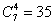 行; 行;因为上述共有98行,所以还有2行各有5个1, 所以此时表格中最少有 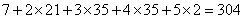 个1, 个1,所以 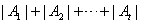 的最小值为304。 的最小值为304。 |


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| a11 | a12 | … | a1m |
| a21 | a22 | … | a2m |
| … | … | … | … |
| an1 | an2 | … | anm |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com