[题目]如图.直三棱柱ABC﹣A1B1C1 . 底面△ABC中.CA=CB=1.∠BCA=90°.棱AA1=2.M.N分别是A1B1.A1A的中点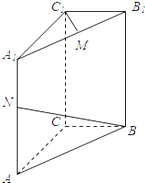． (1)求的长,(2)求cos( )的值,(3)求证A1B⊥C1M．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，直三棱柱ABC﹣A1B1C1 ，底面△ABC中，CA=CB=1，∠BCA=90°，棱AA1=2，M，N分别是A1B1、A1A的中点．

（1）求的长；
（2）求cos（）的值；
（3）求证A1B⊥C1M．

【答案】
（1）解：如图，以C为原点建立空间直角坐标系O﹣xyz．

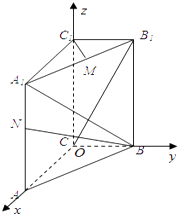
依题意得B（0，1，0），N（1，0，1），

∴

（2）解：依题意得A1（1，0，2），B（0，1，0），C（0，0，0），B1（0，1，2）．

∴ ，，，，

∴cos＜

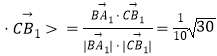
（3）证明：依题意得C1（0，0，2），M =（﹣1，1，﹣2）， = ，

∴ = ，

∴

【解析】由直三棱柱ABC﹣A1B1C1中，由于BCA=90°，我们可以以C为原点建立空间直角坐标系O﹣xyz．（1）求出B点N点坐标，代入空间两点距离公式，即可得到答案；（2）分别求出向量，的坐标，然后代入两个向量夹角余弦公式，即可得到，＞的值；（3）我们求出向量，的坐标，然后代入向量数量积公式，判定两个向量的数量积是否为0，若成立，则表明A1B⊥C1M
【考点精析】关于本题考查的异面直线及其所成的角，需要了解异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能得出正确答案．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=1﹣ 在R上是奇函数．
（1）求a；
（2）对x∈（0，1]，不等式sf（x）≥2x﹣1恒成立，求实数s的取值范围；
（3）令g（x）= ，若关于x的方程g（2x）﹣mg（x+1）=0有唯一实数解，求实数m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列选项中，说法正确的个数是（）

①命题“”的否定为“”；

②命题“在中，，则”的逆否命题为真命题；

③设是公比为的等比数列，则“”是“为递增数列”的充分必要条件；

④若统计数据的方差为，则的方差为；

⑤若两个随机变量的线性相关性越强，则相关系数绝对值越接近1.

A. 1个 B. 2个 C. 3个 D. 4个

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动，其路程fi（x）（i=1，2，3，4）关于时间x（x≥0）的函数关系式分别为f1（x）=2x﹣1，f2（x）=x3 ， f3（x）=x，f4（x）=log2（x+1），有以下结论： ①当x＞1时，甲走在最前面；
②当x＞1时，乙走在最前面；
③当0＜x＜1时，丁走在最前面，当x＞1时，丁走在最前面；
④丙不可能走在最前面，也不可能走在最后面；
⑤如果它们一直运动下去，最终走在最前面的是甲．
其中，正确结论的序号为（把正确结论的序号都填上，多填或少填均不得分）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列命题：
①命题“x∈R，x2+x+1=0”的否定是“x∈R，x2+x+1≠0”；
②若A={x|x＞0}，B={x|x≤﹣1}，则A∩（RB）=A；
③函数f（x）=sin（ωx+φ）（ω＞0）是偶函数的充要条件是φ=kπ+ （k∈Z）；
④若非零向量，满足 =λ ， =λ （λ∈R），则λ=1．
其中正确命题的序号有