|
|
|
如图,圆O为△ABC的外接圆,且AB=AC,过点A的直线交圆O于点D,交BC的延长线于点F,DE是BD的延长线,连接CD.
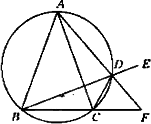
(Ⅰ)求证:∠EDF=∠CDF;
(Ⅱ)求证:AB2=AF·AD.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
对定义在区间l,上的函数f(x),若存在开区间(a,b) I和常数C,使得对任意的x∈(a,b)都有-C<f(x)<C,且对任意的x I和常数C,使得对任意的x∈(a,b)都有-C<f(x)<C,且对任意的x (a,b)都有|f(x)|=C恒成立,则称函数f(x)为区间I上的“Z型”函数. (a,b)都有|f(x)|=C恒成立,则称函数f(x)为区间I上的“Z型”函数.
(Ⅰ)求证:函数f(x)=|x-3|-|x-1|是R上的“Z型”函数;
(Ⅱ)设f(x)是(I)中的“Z型”函数,若不等式|t|=|t+1|≥f(x)对任意的x∈R恒成立,求实数t的取值范围.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
关于函数函数f(x)=2cosx(cosx+ sinx)-1,以下结论正确的是 sinx)-1,以下结论正确的是
|
| [ ] |
A. |
f(x)的最小正周期是π,在区间(- , , )是增函数 )是增函数
|
B. |
f(x)的最小正周期是π,在区间(- , , )是增函数 )是增函数
|
C. |
f(x)的最小正周期是π,最大值是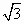
|
D. |
f(x)的最小正周期是2π,最大值是2
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在△ABC中,角A,B,C的对边分别为a,b,c且a+c=10,C=2A,cosA= . .
求:(Ⅰ) 的值; 的值;
(Ⅱ)b的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
下列函数中,在其定义域内既是奇函数又是增函数的是
|
| [ ] |
A. |
y=x+x3
|
B. |
y=3x
|
C. |
y=-log2x
|
D. |
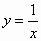
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数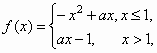 若 若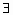 x1x2∈R,x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是 x1x2∈R,x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是
|
| [ ] |
A. |
(-2,2)
|
B. |
(-∞,-2)∪(2,+∞)
|
C. |
(-∞,2)
|
D. |
(-∞,2]
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在区间[0,π]内随机取两个数分别记为a、b,则使得函数f(x)=x2+2ax+b2+π有零点的概率为
|
| [ ] |
A. |
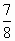
|
B. |
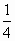
|
C. |
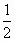
|
D. |
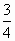
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若集合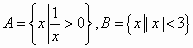 ,则A∩B= ,则A∩B=
|
| [ ] |
A. |
{x|x<0}
|
B. |
{x|0<x<3}
|
C. |
{x|x>4}
|
D. |
R
|
|
|
查看答案和解析>>

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案