练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
我们把正切函数在整个定义域内的图象看作一组“平行曲线”,而“平行曲线”具有性质:任意两条平行于横轴的直线与两条相邻的“平行曲线”相交,被截得的线段长度相等,已知函数 图象中的两条相邻“平行曲线”与直线y=2012相交于A,B两点,且|AB|=2,则 图象中的两条相邻“平行曲线”与直线y=2012相交于A,B两点,且|AB|=2,则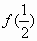 )= )=
|
| [ ] |
A. |

|
B. |

|
C. |

|
D. |
-
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
阅读下面程序框图,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出数对(x,y)的概率为
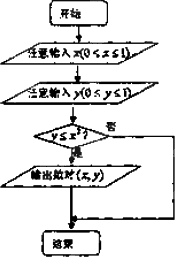
|
| [ ] |
A. |
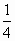
|
B. |
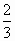
|
C. |
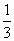
|
D. |
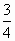
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
椭圆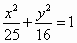 的左右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为 的左右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为
|
| [ ] |
A. |
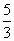
|
B. |
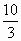
|
C. |
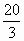
|
D. |
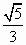
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,圆O为△ABC的外接圆,且AB=AC,过点A的直线交圆O于点D,交BC的延长线于点F,DE是BD的延长线,连接CD.
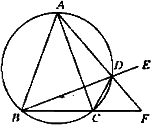
(Ⅰ)求证:∠EDF=∠CDF;
(Ⅱ)求证:AB2=AF·AD.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
执行下图的程序框图,若输出的n=5,则输入整数p的最小值是
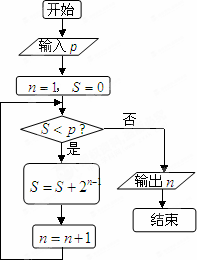
|
| [ ] |
A. |
7
|
B. |
14
|
C. |
15
|
D. |
6
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,圆O为△ABC的外接圆,且AB=AC,过点A的直线交圆O于点D,交BC的延长线于点F,DE是BD的延长线,连接CD.
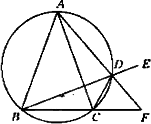
(Ⅰ)求证:∠EDF=∠CDF;
(Ⅱ)求证:AB2=AF·AD.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
从某校高三年级800名学生中随机抽取50名测量身高.据测量,被抽取的学生的身高全部介于155 cm和195 cm之间,将测量结果分成八组得到的频率分布直方图如下:

(1)试估计这所学校高三年级800名学生中身高在180 cm以上(含180 cm)的人数为多少;
(2)在样本中,若学校决定身高在185 cm以上的学生中随机抽取2名学生接受某军校考官进行面试,求:身高在190 cm以上的学生中至少有一名学生接受面试的概率.
|
|
|
查看答案和解析>>
