|
|
|
我们把正切函数在整个定义域内的图象看作一组“平行曲线”,而“平行曲线”具有性质:任意两条平行于横轴的直线与两条相邻的“平行曲线”相交,被截得的线段长度相等,已知函数 图象中的两条相邻“平行曲线”与直线y=2012相交于A,B两点,且|AB|=2,则 图象中的两条相邻“平行曲线”与直线y=2012相交于A,B两点,且|AB|=2,则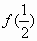 )= )=
|
| [ ] |
A. |

|
B. |

|
C. |

|
D. |
-
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在△OAB(O为原点)中, =(2cosα,2sinα), =(2cosα,2sinα), =(5cosβ,5sinβ),若 =(5cosβ,5sinβ),若 · · =-5,则△OAB的面积S= =-5,则△OAB的面积S=
|
| [ ] |
A. |

|
B. |

|
C. |
5
|
D. |
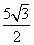
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知x,y满足不等式组 则z=2x+y的最大值与最小值的比值为 则z=2x+y的最大值与最小值的比值为
|
| [ ] |
A. |
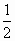
|
B. |
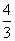
|
C. |
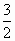
|
D. |
2
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
对定义在区间l,上的函数f(x),若存在开区间(a,b) I和常数C,使得对任意的x∈(a,b)都有-C<f(x)<C,且对任意的x I和常数C,使得对任意的x∈(a,b)都有-C<f(x)<C,且对任意的x (a,b)都有|f(x)|=C恒成立,则称函数f(x)为区间I上的“Z型”函数. (a,b)都有|f(x)|=C恒成立,则称函数f(x)为区间I上的“Z型”函数.
(Ⅰ)求证:函数f(x)=|x-3|-|x-1|是R上的“Z型”函数;
(Ⅱ)设f(x)是(I)中的“Z型”函数,若不等式|t|=|t+1|≥f(x)对任意的x∈R恒成立,求实数t的取值范围.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知x,y满足不等式组 则z=2x+y的最大值与最小值的比值为 则z=2x+y的最大值与最小值的比值为
|
| [ ] |
A. |
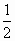
|
B. |
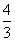
|
C. |
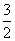
|
D. |
2
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在△ABC中,角A,B,C的对边分别为a,b,c,已知向量m=(cosA,cosB),n=(2c+b,a),且m⊥n.
(Ⅰ)求角A的大小;
(Ⅱ)若a=4,求△ABC面积的最大值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
对定义在区间l,上的函数f(x),若存在开区间(a,b) I和常数C,使得对任意的x∈(a,b)都有-C<f(x)<C,且对任意的x I和常数C,使得对任意的x∈(a,b)都有-C<f(x)<C,且对任意的x (a,b)都有|f(x)|=C恒成立,则称函数f(x)为区间Ⅰ上的“Z型”函数. (a,b)都有|f(x)|=C恒成立,则称函数f(x)为区间Ⅰ上的“Z型”函数.
(Ⅰ)求证:函数f(x)=|x-3|-|x-1|是R上的“Z型”函数;
(Ⅱ)设f(x)是(Ⅰ)中的“Z型”函数,若不等式|t|=|t+1|≥f(x)对任意的x∈R恒成立,求实数t的取值范围.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数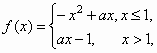 若 若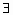 x1x2∈R,x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是 x1x2∈R,x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是
|
| [ ] |
A. |
(-2,2)
|
B. |
(-∞,-2)∪(2,+∞)
|
C. |
(-∞,2)
|
D. |
(-∞,2]
|
|
|
查看答案和解析>>
