
在△ABC中,角A,B,C的对边分别为a,b,c,若acos2 +ccos2
+ccos2 =
= b.
b.
(1)求证:a,b,c成等差数列;
(2)若∠B=60°,b=4,求△ABC的面积.
(1)见解析(2)4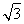
【解析】(1)acos2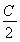 +ccos2
+ccos2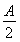 =a·
=a·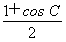 +c·
+c·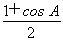 =
= b,
b,
即a(1+cos C)+c(1+cos A)=3b.由正弦定理得:
sin A+sin Acos C+sin C+cos Asin C=3sin B,
即sin A+sin C+sin(A+C)=3sin B,∴sin A+sin C=2sin B.
由正弦定理得,a+c=2b,故a,b,c成等差数列.
(2)由∠B=60°,b=4及余弦定理得:42=a2+c2-2accos 60°,
∴(a+c)2-3ac=16,
又由(1)知a+c=2b,代入上式得4b2-3ac=16,解得ac=16,
∴△ABC的面积S=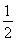 acsin B=
acsin B=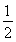 acsin 60°=4
acsin 60°=4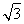 .
.


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第2课时练习卷(解析版) 题型:填空题
已知E,F,G,H是空间四点,命题甲:E,F,G,H四点不共面,命题乙:直线EF和GH不相交,则甲是乙成立的________条件.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(解析版) 题型:选择题
执行如图所示的程序框图,如果依次输入函数:f(x)=3x、f(x)=sin x、f(x)=x3、f(x)=x+ ,那么输出的函数f(x)为( )
,那么输出的函数f(x)为( )

A.3x B.sin x C.x3 D.x+
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
设e1,e2,e3,e4是某平面内的四个单位向量,其中e1⊥e2,e3与e4的夹角为45°,对这个平面内的任意一个向量a=xe1+ye2,规定经过一次“斜二测变换”得到向量a1=xe3+ e4.设向量t1=-3e3-2e4是经过一次“斜二测变换”得到的向量,则|t|是( )
e4.设向量t1=-3e3-2e4是经过一次“斜二测变换”得到的向量,则|t|是( )
A.5 B. C.73 D.
C.73 D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
已知 =1-yi,其中x,y是实数,i是虚数单位,则x+yi的共轭复数为( )
=1-yi,其中x,y是实数,i是虚数单位,则x+yi的共轭复数为( )
A.1+2i B.1-2i C.2+i D.2-i
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第2课时练习卷(解析版) 题型:选择题
已知cos α= ,cos(α+β)=-
,cos(α+β)=- ,且α,β∈
,且α,β∈ ,则cos(α-β)的值等于( )
,则cos(α-β)的值等于( )
A.- B.
B. C.-
C.- D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:解答题
函数f(x)=Asin  +1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为 .
.
(1)求函数f(x)的解析式;
(2)设α∈ ,f
,f  =2,求α的值.
=2,求α的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:填空题
设函数y=f(x),x∈R的导函数为f′(x),且f(x)=f(-x),f′(x)<f(x).则下列三个数:ef(2),f(3),e2f(-1)从小到大依次排列为________.(e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:选择题
已知偶函数f(x)当x∈[0,+∞)时是单调递增函数,则满足f( )<f(x)的x的取值范围是( )
)<f(x)的x的取值范围是( )
A.(2,+∞) B.(-∞,-1)
C.[-2,-1)∪(2,+∞) D.(-1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com