
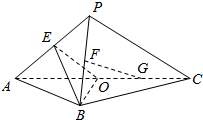
 如图,E、F、O分别是PA,PB,AC的中点,G是OC的中点,求证:FG∥平面BOE(两种方法证明).
如图,E、F、O分别是PA,PB,AC的中点,G是OC的中点,求证:FG∥平面BOE(两种方法证明). 分析 【方法一】取PE的中点H,连接FH,GH,证明平面FHG∥平面BEO,从而得出FG∥平面BOE;
【方法二】连接AF,交BE于点M,连接OM,证明MO∥FG,从而证明FG∥平面BOE.
解答 证明:【方法一】取PE的中点H,连接FH,GH,如图1所示: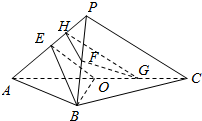
E、F、O分别是PA,PB,AC的中点,G是OC的中点,
∴HF∥EB,HG∥EO;
又HF?平面BEO,HG?平面BEO,
EB?平面BEO,EO?平面BEO,
∴HF∥平面BEO,HG∥平面BEO;
又HF∩HG=H,HF?平面FHG,HG?平面FHG,
∴平面FHG∥平面BEO,
又FG?平面FHG,
∴FG∥平面BOE.
【方法二】连接AF,交BE于点M,连接OM,
如图2所示: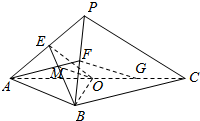
∵E、F、O分别是PA,PB,AC的中点,G是OC的中点,
∴$\frac{AM}{MF}$=$\frac{AO}{OG}$=$\frac{2}{1}$,
∴MO∥FG;
又MO?平面BOE,FG?平面BOE,
∴FG∥平面BOE.
点评 本题考查了空间中的线面平行的证明问题,也考查了空间想象能力与逻辑思维能力,是中档题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
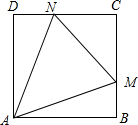 如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )
如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )| A. | 4($\sqrt{2}$-1) | B. | 8($\sqrt{2}$-1) | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程$\frac{y}{x-2}=1$表示斜率为1,在y轴上截距为-2的直线 | |
| B. | △ABC的三个顶点是A(-3,0),B(3,0),C(0,3),则中线CO(O为坐标原点)的方程是x=0 | |
| C. | 到y轴距离为2的点的轨迹方程为x=2 | |
| D. | 方程y=$\sqrt{{x}^{2}+2x+1}$表示两条射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=4 | B. | a=6 | C. | a≤6 | D. | a≥6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com