
【题目】已知无穷数列{an},a1=1,a2=2,对任意n∈N* , 有an+2=an , 数列{bn}满足bn+1﹣bn=an(n∈N*),若数列 ![]() 中的任意一项都在该数列中重复出现无数次,则满足要求的b1的值为
中的任意一项都在该数列中重复出现无数次,则满足要求的b1的值为
【答案】2
【解析】解:a1=1,a2=2,对任意n∈N* , 有an+2=an , ∴a3=a1=1,a4=a2=2,a5=a3=a1=1,
∴an= ![]()
∴bn+1﹣bn=an= ![]() ,
,
∴b2n+2﹣b2n+1=a2n+1=1,b2n+1﹣b2n=a2n=2,
∴b2n+2﹣b2n=3,b2n+1﹣b2n﹣1=3
∴b3﹣b1=b5﹣b3=…=b2n+1﹣b2n﹣1=3,
b4﹣b2=b6﹣b4=b8﹣b6=…=b2n﹣b2n﹣2=3,b2﹣b1=1,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() =b4n﹣2 ,
=b4n﹣2 , ![]() ,
,
∵数列 ![]() 中的任意一项都在该数列中重复出现无数次,
中的任意一项都在该数列中重复出现无数次,
∴b2=b6=b10=…=b2n﹣1 ,
b4=b8=b12=…=b4n ,
解得b8=b4=3,
b2=3,∵b2﹣b1=1,∴b1=2,
所以答案是:2
【考点精析】根据题目的已知条件,利用数列的定义和表示的相关知识可以得到问题的答案,需要掌握数列中的每个数都叫这个数列的项.记作an,在数列第一个位置的项叫第1项(或首项),在第二个位置的叫第2项,……,序号为n的项叫第n项(也叫通项)记作an.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x2)+ax.(a≤0)
(1)若f(x)在x=0处取得极值,求a的值;
(2)讨论f(x)的单调性;
(3)证明:(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<
)< ![]() (n∈N* , e为自然对数的底数).
(n∈N* , e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆x2+ ![]() =1的左、右顶点分别为A、B,双曲线Γ以A、B为顶点,焦距为2
=1的左、右顶点分别为A、B,双曲线Γ以A、B为顶点,焦距为2 ![]() ,点P是Γ上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为k,O为坐标原点.
,点P是Γ上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为k,O为坐标原点. 
(1)求双曲线Γ的方程;
(2)求点M的纵坐标yM的取值范围;
(3)是否存在定直线l,使得直线BP与直线OM关于直线l对称?若存在,求直线l方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为15°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值为 . 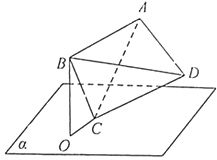
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com