
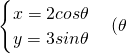 为参数)和极坐标方程ρ=4sinθ所表示的图形分别是
为参数)和极坐标方程ρ=4sinθ所表示的图形分别是 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:
 A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:| PB |
| PA |
| 1 |
| 2 |
| PC |
| PD |
| 1 |
| 3 |
| BC |
| AD |
|
| 2 |
| cosθ-sinθ |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
查看答案和解析>>
科目:高中数学 来源:2011届福建省宁德市高三普通班质量检测理科数学 题型:解答题
(2)(本小题满分7分)选修4—4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(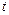 为参数),若圆
为参数),若圆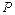 在以该直
在以该直 角坐标系的原点
角坐标系的原点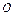 为极点、
为极点、 轴的正半轴为极轴的极坐标系下的方程为
轴的正半轴为极轴的极坐标系下的方程为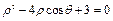
 .
.
(Ⅰ)求曲线 的普通方程和圆
的普通方程和圆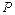 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点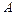 是曲线
是曲线 上的动点,点
上的动点,点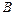 是圆
是圆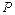 上的动点,求
上的动点,求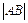 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2012届宁夏银川一中高三上学期第二次月考理科数学试卷 题型:解答题
(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系中,以原点为极点,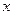 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线
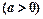 ,已知过点
,已知过点 的直线
的直线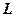 的参数方程为:
的参数方程为: ,直线
,直线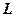 与曲线
与曲线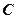 分别交于
分别交于 .
.
(1)写出曲线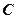 和直线
和直线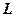 的普通方程;
的普通方程;
(2)若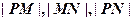 成等比数列,求
成等比数列,求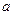 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com