
分析 (1)根据定义设:h(x+T)=T•h(x),得出x+T=T•x对任意x恒成立,显然不成立;
(2)根据定义设:h(x+T)=T•h(x),得出 ${({\frac{1}{4}})^{x+T}}=T•{({\frac{1}{4}})^x}$对任意x恒成立,可得 ${({\frac{1}{4}})^T}=T$,求解T,并判断唯一性即可;
(3)若f(n)是2倍周期函数,f(3)=f(1+2)=2f(1)=2,f(4)=f(2+2)=2f(2)=-8,同理可求出f(2n-1)=f(2n-3+2)=2f(2n-3)=2n-1,进而求出,${C_n}=\frac{{{S_{2n}}}}{{{S_{2n-1}}}}=\frac{{3({{2^n}-1})}}{{{2^n}-3}}$,通过比值判断Cn的单调性,进而求出Cn的最大值,最后得出loga(a+1)>-1,分别讨论a的不同情况,求出a的取值范围.
解答 (1)设:h(x+T)=T•h(x)
则 x+T=T•x对任意x恒成立 (2分)
∵T无解
∴h(x)=x不是T倍周期函数 (2分)
(2)设:g(x+T)=T•g(x)
则 ${({\frac{1}{4}})^{x+T}}=T•{({\frac{1}{4}})^x}$对任意x恒成立 (2分)
${({\frac{1}{4}})^T}=T$,
$T=\frac{1}{2}$(2分)
下证唯一性:
若$T>\frac{1}{2}$,$T={({\frac{1}{4}})^T}<{({\frac{1}{4}})^{\frac{1}{2}}}=\frac{1}{2}$矛盾
若$T<\frac{1}{2}$,$T={({\frac{1}{4}})^T}>{({\frac{1}{4}})^{\frac{1}{2}}}=\frac{1}{2}$矛盾
∴$T=\frac{1}{2}$是唯一的 (2分)
(3)f(3)=f(1+2)=2f(1)=2,
f(5)=f(3+2)=2f(3)=22
f(7)=f(5+2)=2f(5)=23…
f(2n-1)=f(2n-3+2)=2f(2n-3)=2n-1
f(1)+f(3)+f(5)+…+f(2n-1)=1+2+22+…+2n-1=2n-1 (2分)
同理:f(2)+f(4)+f(6)+…+f(2n)=-4(1+2+22+…+2n-1)=-4(2n-1)
∴${S_{2n}}=f(1)+f(2)+…+f({2n})=-3({{2^n}-1})$
同理:${S_{2n-1}}=f(1)+f(2)+…+f({2n-1})=-{2^n}+3$,
${C_n}=\frac{{{S_{2n}}}}{{{S_{2n-1}}}}=\frac{{3({{2^n}-1})}}{{{2^n}-3}}$(2分)
C1=-3C2=9
显然:n≥2Cn>0且 $\frac{{{C_{n+1}}}}{C_n}=\frac{{\frac{{3({{2^{n+1}}-1})}}{{{2^{n+1}}-3}}}}{{\frac{{3({{2^n}-1})}}{{{2^n}-3}}}}=\frac{{2{{({2^n})}^2}-7•({2^n})+3}}{{2{{({2^n})}^2}-5•({2^n})+3}}$
∵2(2n)2-7•(2n)+3<2(2n)2-5•(2n)+3
∴$\frac{{{C_{n+1}}}}{C_n}<1$即单调递减
∴(Cn)max=C1=9 (2分)
∵Cn<loga(a+1)+10恒成立,
∴loga(a+1)+10>(Cn)max=9
∴loga(a+1)>-1
①a>1时 $a+1>\frac{1}{a}$解得:a>1
②0<a<1时 $a+1<\frac{1}{a}$解得:$0<a<\frac{{-1+\sqrt{5}}}{2}$,
∴$0<a<\frac{{-1+\sqrt{5}}}{2}$或 a>1 (2分)
点评 本题综合性强,考查了对新定义的理解,利用新定义,结合数列解决恒成立问题.属于难度较大的题型.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
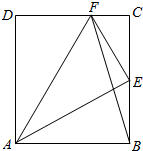 如图,在矩形ABCD中,点E是BC边上中点,点F在边CD上.
如图,在矩形ABCD中,点E是BC边上中点,点F在边CD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com